题目内容
3.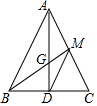 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.
分析 过M作ME⊥BC于点E,则只要求得GD:ME的值即可,由中位线定理可知MD=$\frac{1}{2}$AD,由重心的性质可知GD=$\frac{1}{3}$AD,则可求得答案.
解答 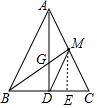 解:
解:
如图,过M作ME⊥BC于点E,
∵AB=AC,AD⊥BC,
∴D为BC中点,AD为BC边上的中线,
∵M为AC的中点,
∴MD=$\frac{1}{2}$AD,
∴G为△ABC的重心,
∴GD=$\frac{1}{3}$AD,
∴$\frac{{S}_{△GBD}}{{S}_{△MDC}}$=$\frac{\frac{1}{2}BD•GD}{\frac{1}{2}CD•ME}$=$\frac{GD}{ME}$=$\frac{\frac{1}{3}AD}{\frac{1}{2}AD}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题主要考查三角形中位线和重心的性质,掌握三角形的中位线等于第三边的一半、三角形重心是中线的三等分点是解题的关键.

练习册系列答案
相关题目
18.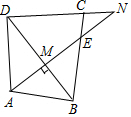 如图,在四边形ABCD中,AD=CD,∠ADC=90°,N为DC的延长线上一点,AN⊥BD于点M,交BC于点E,且∠BAN=45°,下列结论:
如图,在四边形ABCD中,AD=CD,∠ADC=90°,N为DC的延长线上一点,AN⊥BD于点M,交BC于点E,且∠BAN=45°,下列结论:
①∠CBD=45°;②$\sqrt{2}$BD-AB=BC;③若BE=2CE,则S△BCD=6S△CEN.
其中结论正确的个数有( )
 如图,在四边形ABCD中,AD=CD,∠ADC=90°,N为DC的延长线上一点,AN⊥BD于点M,交BC于点E,且∠BAN=45°,下列结论:
如图,在四边形ABCD中,AD=CD,∠ADC=90°,N为DC的延长线上一点,AN⊥BD于点M,交BC于点E,且∠BAN=45°,下列结论:①∠CBD=45°;②$\sqrt{2}$BD-AB=BC;③若BE=2CE,则S△BCD=6S△CEN.
其中结论正确的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.单项式-4ab2的系数是( )
| A. | 4 | B. | -4 | C. | 3 | D. | 2 |
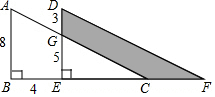 如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.求图中阴影部分的面积.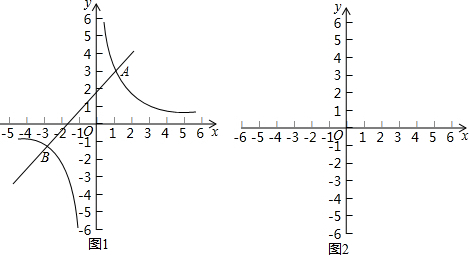
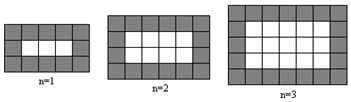
 如图,下面几何体由四个大小相同的小立方块组成,则它的左视图是( )
如图,下面几何体由四个大小相同的小立方块组成,则它的左视图是( )



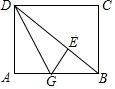 如图:矩形纸片ABCD中,AB=4,AD=3折叠纸片.使AD边与对角线BD重合,点A落在点E处,折痕为DG,求AG的长.
如图:矩形纸片ABCD中,AB=4,AD=3折叠纸片.使AD边与对角线BD重合,点A落在点E处,折痕为DG,求AG的长.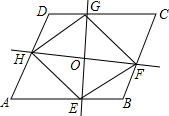 如图,过?ABCD中对角线的中点O作两条互相垂直的直线,分别交AB、BC、CD、DA于E、F、G、H,试判断四边形EFGH的形状并说明理由.
如图,过?ABCD中对角线的中点O作两条互相垂直的直线,分别交AB、BC、CD、DA于E、F、G、H,试判断四边形EFGH的形状并说明理由.