题目内容
5.九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
分析 (1)①售价-进价即可得;②待定系数法求解可得;
(2)根据总利润=单件利润×销售量,列一元二次方程求解可得;
(3)根据(2)中相等关系列出函数解析式,根据二次函数的性质可得.
解答 解:(1)由题意知销售该图书每本的利润是x-30元,
设月销量m与售价x间的函数关系式为m=kx+b,
由题意得:$\left\{\begin{array}{l}{50k+b=2000}\\{60k+b=1600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-40}\\{b=4000}\end{array}\right.$,
∴月销量m=-40x+4000,
故答案为:①x-30;②-40x+4000;
(2)根据题意可得(x-30)(-40x+4000)=48000,
解得:x=60或x=70,
答:若销售图书的月利润为48000元,则每本图书需要售价60元或70元;
(3)y=(x-30)(-40x+4000)
=-40(x-65)2+49000,
∴售价为65元时,当月的利润最大,最大利润是49000元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式及根据相等关系列出方程或函数解析式是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
13.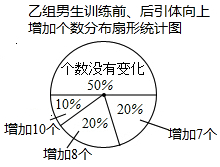 某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
甲组男生训练前、后引体向上个数统计表(单位:个)
(1)根据以上信息,解答下列问题:
(1)a=7,b=4,c=6.5;
(2)甲组训练后引体向上的平均个数比训练前增长了75%;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占到该组人数的50%,所以乙组的平均个数不可能提高4个之多.:你同意他的观点吗?说明理由.
 某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.甲组男生训练前、后引体向上个数统计表(单位:个)
| 甲组 | 男生A | 男生B | 男生C | 男生D | 男生E | 男生F | 平均个数 | 众数 | 中位数 |
| 训练前 | 4 | 6 | 4 | 3 | 5 | 2 | 4 | b | 4 |
| 训练后 | 8 | 9 | 6 | 6 | 7 | 6 | a | 6 | c |
(1)a=7,b=4,c=6.5;
(2)甲组训练后引体向上的平均个数比训练前增长了75%;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占到该组人数的50%,所以乙组的平均个数不可能提高4个之多.:你同意他的观点吗?说明理由.
12.单项式-4ab2的系数是( )
| A. | 4 | B. | -4 | C. | 3 | D. | 2 |

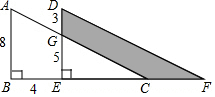 如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.求图中阴影部分的面积.