题目内容
2.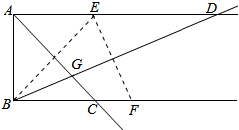 已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1.
已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1.
分析 根据轴对称的性质可得∠BAC=∠DAC,AB=AE,然后求出△ABE是等腰直角三角形,再根据等腰直角三角形的性质求出∠ABE=45°,再根据轴对称的性质可得∠DBE=∠DBF,根据两直线平行,内错角相等可得∠DBF=∠ADB,从而得到∠ADB=∠DBE,再根据等边对等角可得BE=DE,然后用AB表示出DE、AD,再根据锐角的正切等于对边比邻边列式计算即可得解.
解答 解:∵点E与点B关于AC对称,
∴∠BAC=∠DAC,AB=AE,
又∵AB⊥AD,
∴△ABE是等腰直角三角形,
∴∠ABE=45°,
∵点E点F关于BD对称,
∴∠DBE=∠DBF,
∵AD∥BC,
∴∠DBF=∠ADB,
∴∠ADB=∠DBE,
∴BE=DE,
在△ABE中,BE=$\sqrt{2}$AB,
∴DE=$\sqrt{2}$AB,
∴AD=AE+DE=AB+$\sqrt{2}$AB=($\sqrt{2}$+1)AB,
∴tan∠ADB=$\frac{AB}{AD}$=$\frac{AB}{(\sqrt{2}+1)AB}$=$\sqrt{2}$-1.
故答案为:$\sqrt{2}$-1.
点评 本题考查了轴对称的性质,等腰直角三角形的判定与性质,锐角三角函数的定义,熟记各性质并准确识图,用AB表示出AD是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
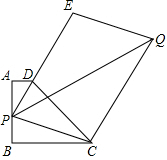 已知梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,以PE、PC为边作?PCQE,则对角线PQ的最小值为7.
已知梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,以PE、PC为边作?PCQE,则对角线PQ的最小值为7. 如图,在△ABC中,DE∥CB,若AD:DC=3:1,EB=2,则AE=6.
如图,在△ABC中,DE∥CB,若AD:DC=3:1,EB=2,则AE=6. 如图,D为圆O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为圆O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3.
如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3.