题目内容
14. 如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3.
如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3.
分析 根据平行线分线段成比例定理,由DE∥BC得到$\frac{AD}{BD}$=$\frac{AE}{EC}$,然后把EC=2AE,BD=6代入后利用比例的性质计算即可.
解答 解:∵DE∥BC,
∴$\frac{AD}{BD}$=$\frac{AE}{EC}$,
∵EC=2AE,BD=6,
∴$\frac{AD}{6}$=$\frac{AE}{2AE}$=$\frac{1}{2}$,
∴AD=3.
故答案为3.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
相关题目
5.下列图形中,①正方形,②长方形,③等边三角形,④线段⑤角,绕某个点旋转180°能与自身重合的有( )
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.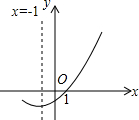 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )
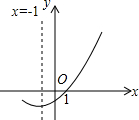 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )| A. | -2,1 | B. | -3,1 | C. | -1,1 | D. | 不能确定 |
19. 如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
 如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )| A. | △ABO≌△DCO | B. | AO=DO | C. | AC=DB | D. | BD平分∠ABC |
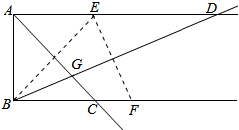 已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1.
已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1. 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GDM:S△GAB的值为1:4.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GDM:S△GAB的值为1:4.