题目内容
12.如果方程组 $\left\{\begin{array}{l}{3m+n=3a+2}\\{m+2n=2-a}\end{array}\right.$的解满足m+n≤6,求a的取值范围.分析 由方程(①+②×2)÷5得到m+n的值,根据m+n≤6.求出a的取值范围.
解答 解:$\left\{\begin{array}{l}{3m+n=3a+2①}\\{m+2n=2-a②}\end{array}\right.$
(①+②×2)÷5得,
m+n=$\frac{a+6}{5}$,
$\frac{a+6}{5}$≤6,
解得a≤24.
点评 本题考查的是二元一次方程组的解法和一元一次不等式的解法,求出m+n的值列出不等式是解题的关键.

练习册系列答案
相关题目
20.我们学习了圆周角定理,回顾学习过程,在探索同弧所对的圆周角和圆心角的关系时,主要体现的数学思想是( )
| A. | 转化 | B. | 数形结合 | C. | 演绎 | D. | 分类讨论 |
17.已知P(2t+1,3t-2)是第四象限内的整点(模拟坐标都为整数的点称为整点),则P的坐标为( )
| A. | (1,-2) | B. | (1,2) | C. | (-2,-1) | D. | (2,-1) |
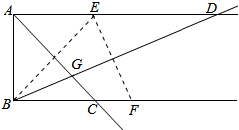 已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1.
已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1. 如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题.
如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题. 已知a,b,c在数轴上对应点的位置如图所示,化简:|a|-|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|.
已知a,b,c在数轴上对应点的位置如图所示,化简:|a|-|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|.