题目内容
10.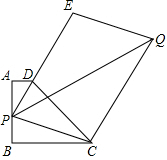 已知梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,以PE、PC为边作?PCQE,则对角线PQ的最小值为7.
已知梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,以PE、PC为边作?PCQE,则对角线PQ的最小值为7.
分析 设PQ与DC相交于点G,作QH⊥BC,交BC的延长线于H,由PE∥CQ,DE=2PD,可得$\frac{DG}{GC}=\frac{PD}{CQ}=\frac{1}{3}$,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案.
解答  解:设PQ与DC相交于点G,
解:设PQ与DC相交于点G,
∵PE∥CQ,DE=2PD,
∴$\frac{DG}{GC}$=$\frac{PD}{CQ}$=$\frac{1}{3}$,
∴G是DC上一定点,
作QH⊥BC,交BC的延长线于H,
同理可证∠ADP=∠QCH,
∴Rt△ADP∽Rt△HCQ,
即$\frac{AD}{CH}$=$\frac{PD}{CQ}$=$\frac{1}{3}$,
∴CH=3,
∴BH=BC+CH=4+3=7,
∴当PQ⊥AB时,PQ的长最小,即为7.
故答案为:7.
点评 考查了相似三角形的判定与性质、直角梯形的性质、平行四边形的性质、矩形的性质,注意准确作出辅助线是解此题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.二次函数y=x2-2x-3与y轴的交点坐标为( )
| A. | 无交点 | B. | (0,-1) | C. | (-3,0) | D. | (0,-3) |
5.下列图形中,①正方形,②长方形,③等边三角形,④线段⑤角,绕某个点旋转180°能与自身重合的有( )
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
19. 如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
 如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )| A. | △ABO≌△DCO | B. | AO=DO | C. | AC=DB | D. | BD平分∠ABC |
20.我们学习了圆周角定理,回顾学习过程,在探索同弧所对的圆周角和圆心角的关系时,主要体现的数学思想是( )
| A. | 转化 | B. | 数形结合 | C. | 演绎 | D. | 分类讨论 |

 已知A、B、C在一直线上,X、Y、Z在一直线上,并且AY∥BZ,BX∥CY,求证:AX∥CZ.
已知A、B、C在一直线上,X、Y、Z在一直线上,并且AY∥BZ,BX∥CY,求证:AX∥CZ.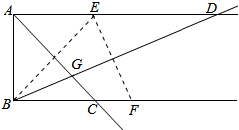 已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1.
已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1.