题目内容
11.如图1,l1∥l2∥l3直线AB和CH交于O点,分别交l2于D,E两点,已知CE=6,HE=3,AB=12.(1)尝试探究在图1中,求出DB和AD的长;
(2)类比延伸:平移AB使得A与H重合,如图2所示,过点D作DF∥AC,若DE=5,求线段BF的长;
(3)拓展迁移:如图3,若某个三角形ABC的面积是10,点D,E分别位于AB,CA上,DE∥BC,点F在BC上且BF=2,CF=3,如果△CBE的面积和四边形FCED的面积相等,求这个相等的面积值.
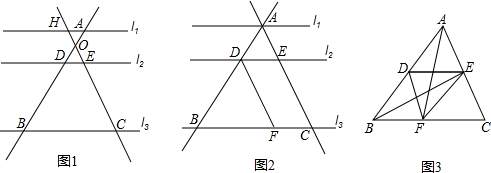
分析 (1)如图1,根据平行线分线段成比例定理,由l1∥l2∥l3得$\frac{AD}{AB}$=$\frac{HE}{HC}$,则利用比例性质可计算出AD=4,于是DB=AB-AD=8;
(2)如图2,由平移性质得BD=8,AD=4,再证明四边形DECF为平行四边形,得到DE=CF=5,根据平行线分线段成比例定理,由DF∥AC得到$\frac{BF}{FC}$=$\frac{BD}{AD}$,利用比例性质可计算BF;
(3)如图3,利用△CBE的面积和四边形FCED的面积相等可得S△BEF=S△DEF,根据三角形面积公式和平行线的判定可得EF∥BD,则根据平行线分线段成比例定理得$\frac{CE}{AE}$=$\frac{CF}{FB}$=$\frac{3}{2}$,然后再利用三角形面积公式可计算出S△CBE=$\frac{3}{5}$S△ABC=6.
解答 解:(1)如图1,∵l1∥l2∥l3,
∴$\frac{AD}{AB}$=$\frac{HE}{HC}$,即$\frac{AD}{12}$=$\frac{3}{3+6}$,
∴AD=4,
∴DB=AB-AD=12-4=8;
(2)如图2,
∵平移AB使得A与H重合,
∴BD=8,AD=4,
∵DF∥AC,
而DE∥CF,
∴四边形DECF为平行四边形,
∴DE=CF=5,
∵DF∥AC,
∴$\frac{BF}{FC}$=$\frac{BD}{AD}$,即$\frac{BF}{5}$=$\frac{8}{4}$,
∴BF=10;
(3)如图3,
∵△CBE的面积和四边形FCED的面积相等,
即S△BEF+S△CEF=S△CEF+S△DEF,
∴S△BEF=S△DEF,
∴EF∥BD,
∴$\frac{CE}{AE}$=$\frac{CF}{FB}$=$\frac{3}{2}$,
∴S△CBE=$\frac{3}{5}$S△ABC=$\frac{3}{5}$×10=6,
即这个相等的面积值为6.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.也考查了平移的性质和三角形面积公式.

 阅读快车系列答案
阅读快车系列答案| A. | 无交点 | B. | (0,-1) | C. | (-3,0) | D. | (0,-3) |
 如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )| A. | △ABO≌△DCO | B. | AO=DO | C. | AC=DB | D. | BD平分∠ABC |
| A. | 转化 | B. | 数形结合 | C. | 演绎 | D. | 分类讨论 |
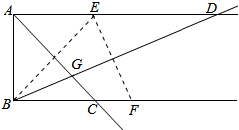 已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1.
已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则tan∠ADB=$\sqrt{2}$-1. 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GDM:S△GAB的值为1:4.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GDM:S△GAB的值为1:4.