题目内容
7. 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.求证:MN=AC.
分析 欲证明MN=AC,只要证明四边形ACMN是平行四边形即可.
解答 证明:在Rt△ABC中,∠C=90°,∵M是AB的中点,
∴CM=$\frac{1}{2}$AB,
∵AN=$\frac{1}{2}$AB,
∴CM=AN,
∵AN∥CM,
∴四边形ACMN是平行四边形.
∴MN=AC.
点评 本题考查平行四边形的判定和性质、直角三角形斜边中线定理,熟练掌握这些性质是解决问题的关键,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.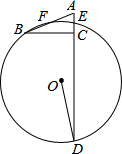 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 13 | B. | $2\sqrt{26}$ | C. | $3\sqrt{26}$ | D. | $\frac{27}{2}$ |
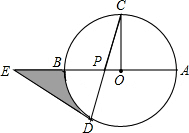 如图,⊙O的半径OC与直径AB垂直,点P在OB上,CP的延长线交⊙O于点D,在OB的延长线上取点E,使ED=EP.
如图,⊙O的半径OC与直径AB垂直,点P在OB上,CP的延长线交⊙O于点D,在OB的延长线上取点E,使ED=EP.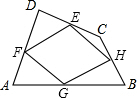 如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.
如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.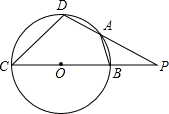 如图,BC为⊙O的直径,D,A是⊙O上两点,延长DA交CB延长线于点P,连接CD,AB.
如图,BC为⊙O的直径,D,A是⊙O上两点,延长DA交CB延长线于点P,连接CD,AB.