题目内容
2.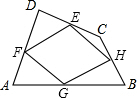 如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.
如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.
分析 根据矩形的判定定理:有一个角为直角的平行四边形是矩形解答,先证四边形EFGH是平行四边形,要使四边形EFGH为矩形,需要∠EFG=90°,即AC⊥BD.
解答 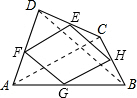 解:依题意得,四边形EFGH是由四边形ABCD各边中点连接而成,
解:依题意得,四边形EFGH是由四边形ABCD各边中点连接而成,
连接AC、BD,
∵E、F、G、H分别是CD、DA、AB、BC的中点,
∴EF∥AC∥HG,EH∥BD∥FG,
∴四边形EFGH是平行四边形,
要使四边形EFGH为矩形,
根据矩形的判定:有一个角为直角的平行四边形是矩形,
故当AC⊥BD时,∠EFG=∠EHG=90°时,四边形EFGH为矩形.
故答案为:AC⊥BD.
点评 本题考查了矩形的判定定理:有一个角是直角的平行四边形是矩形\有三个角是直角的四边形是矩形.\对角线互相平分且相等的四边形是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列运算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\root{3}{4}$=2 | ||
| C. | (x+2y)2=x2+2xy+4y2 | D. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ |
14.下列各式不是多项式a4-1的因式的是( )
| A. | a-1 | B. | a+1 | C. | (a-1)2 | D. | a2+1 |
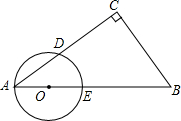 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A. 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM. 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE交CD于F点,∠E=36°,求∠AFC的度数.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE交CD于F点,∠E=36°,求∠AFC的度数.