题目内容
15.已知a=2,b=3,计算$\frac{{a}^{2}+ab}{{b}^{2}}•\frac{{a}^{2}-ab}{{a}^{2}-{b}^{2}}$的值.分析 先把分子分母因式分解,再约分得到原式=$\frac{{a}^{2}}{{b}^{2}}$,然后把a和b的值代入计算即可.
解答 解:原式=$\frac{a(a+b)}{{b}^{2}}$•$\frac{a(a-b)}{(a+b)(a-b)}$
=$\frac{{a}^{2}}{{b}^{2}}$,
当a=2,b=3时,原式=$\frac{{2}^{2}}{{3}^{2}}$=$\frac{4}{9}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
5.已知点P(x,y)的坐标满足|x|=3,$\sqrt{y}$=2,且xy<0,则点P的坐标是( )
| A. | (3,-2) | B. | (-3,2) | C. | (3,-4) | D. | (-3,4) |
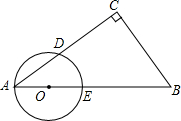 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A. 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.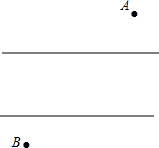 如图,有两个村庄A和B被一条河隔开,现在要架一座桥MN,使得由A到B的路程最短,问桥应架在什么地方?(河岸是平行的,桥垂直于两岸)
如图,有两个村庄A和B被一条河隔开,现在要架一座桥MN,使得由A到B的路程最短,问桥应架在什么地方?(河岸是平行的,桥垂直于两岸)