题目内容
18．已知一个等腰三角形的顶角为x°．底角为y°．（1）请写出y与x之间的函数关系式．并求出自变量x的取值范围．
（2）画出这个函数的图象．
分析 （1）根据三角形内角和定理及等腰三角形两底角相等可得y关于x的函数关系式；
（2）结合自变量取值范围，确定两点画线可得．
解答 解：（1）由三角形内角和等于180°可知：，x+2y=180，
∴y=-$\frac{1}{2}$x+90．
∵等腰三角形的顶角为x°，
∴0＜x＜180．
故y与x之间的函数关系式为y=-$\frac{1}{2}$x+90（0＜x＜180）．
（2）画出图象如下：
点评 本题主要考查根据实际问题列函数关系式及图象的画法，了解内角和定理及等腰三角形性质是基础，根据题意列函数关系式是考查内容．
练习册系列答案
相关题目
8．某工厂现在平均每天比原计划多生产50台机器，现在生产800台所需时间与原计划生产600台机器所需时间相同．设原计划平均每天生产x台机器，根据题意，下面所列方程正确的是（ ）
| A． | $\frac{800}{x+50}$=$\frac{600}{x}$ | B． | $\frac{800}{x-50}$=$\frac{600}{x}$ | C． | $\frac{800}{x}$=$\frac{600}{x+50}$ | D． | $\frac{800}{x}$=$\frac{600}{x-50}$ |
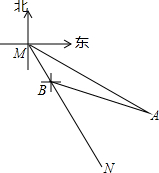如图，东站枢纽建设要新建一条从M地到N地的公路，测得N点位于M点的南偏东30°，A点位于M点的南偏东60°，以A点为中心，半径为500米的圆形区域为文物保护区，又在B点测得BA的方向为南偏东75°，量得MB=400米，请计算后回答公路是否会穿越文物保护区（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）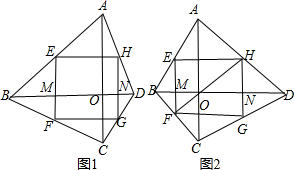
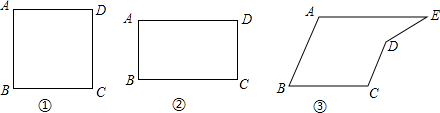
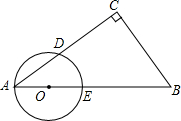已知：如图，在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC，AB分别交于点D，E，且∠CBD=∠A．
已知：如图，Rt△ABC中，∠C=90°，M是AB的中点，AN=$\frac{1}{2}$AB，AN∥CM．