题目内容
19.观察下列式子.猜想规律并完成问题:12+22>2×1×2;
($\sqrt{2}$)2+($\frac{1}{2}$)2>2×$\sqrt{2}×\frac{1}{2}$
(-2)2+32>2×(-2)×3;
($\sqrt{8}$)2+($\sqrt{2}$)2>2×$\sqrt{8}$×$\sqrt{2}$
…
(1)a2+b2>2ab(a≠b);
(2)根据上述规律,试求出代数式x+$\frac{1}{x}$(x>0)的最小值.
分析 (1)根据题目中给出的式子,可以发现其规律,从而可以得到a2+b2与2ab的关系;
(2)根据上面的规律,通过讨论x≠$\frac{1}{x}$和x=$\frac{1}{x}$,可以得到代数式x+$\frac{1}{x}$(x>0)的最小值.
解答 解:(1)由题目可得,a≠b,
a2+b2>2×a×b=2ab,
即a2+b2>2ab.
故答案为:>;
(2)根据上面的规律可知,当x≠$\frac{1}{x}$,x>0时,x+$\frac{1}{x}$>2×$\sqrt{x}×\frac{1}{\sqrt{x}}$=2,
当$x=\frac{1}{x}$,x>0时,得x=1,则$x+\frac{1}{x}=1+1=2$,
即代数式x+$\frac{1}{x}$(x>0)的最小值是2.
点评 本题考查完全平方公式,解题的关键是明确题意,发现其中的规律,利用分类讨论的数学思想求得所要求得问题答案.

练习册系列答案
相关题目
14.下列各式不是多项式a4-1的因式的是( )
| A. | a-1 | B. | a+1 | C. | (a-1)2 | D. | a2+1 |
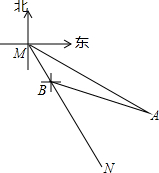 如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)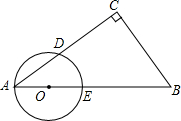 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A. 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.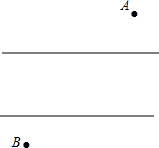 如图,有两个村庄A和B被一条河隔开,现在要架一座桥MN,使得由A到B的路程最短,问桥应架在什么地方?(河岸是平行的,桥垂直于两岸)
如图,有两个村庄A和B被一条河隔开,现在要架一座桥MN,使得由A到B的路程最短,问桥应架在什么地方?(河岸是平行的,桥垂直于两岸)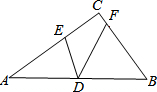 如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2$\sqrt{2}$,DF=4,则AB的长为4$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2$\sqrt{2}$,DF=4,则AB的长为4$\sqrt{5}$.