题目内容
17.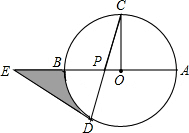 如图,⊙O的半径OC与直径AB垂直,点P在OB上,CP的延长线交⊙O于点D,在OB的延长线上取点E,使ED=EP.
如图,⊙O的半径OC与直径AB垂直,点P在OB上,CP的延长线交⊙O于点D,在OB的延长线上取点E,使ED=EP.(1)求证:ED是⊙O的切线;
(2)当P为OE的中点,且OC=2时,求图中阴影部分的面积.
分析 (1)首先连接OD,ED=EP,易证得∠APD=∠ADP,又由⊙O的半径OC与直径AB垂直,可证得OD⊥ED,即可判定ED是⊙O的切线;
(2)由S阴影=S△ODE-S扇形,即可求得答案.
解答  (1)证明:连接OD,
(1)证明:连接OD,
∵OD是圆的半径,
∴OD=OC.
∴∠CDO=∠DCO.
∵OC⊥AB,
∴∠COP=90°,
∵在Rt△OPC中,∠CPO+∠PCO=90°,
∵ED=EP,
∴∠EDP=∠EPD=∠CPO,
∴∠EDO=∠EDP+∠CDO=∠CPO+∠DCO=90°.
∴ED⊥OD,
即ED是圆的切线;
(2)解:∵P为OE的中点,ED=EP,且由(1)知△ODE为Rt△,
∴PE=PD=ED,
∴∠E=60°,
∵OD=OC=2,
∴ED=$\frac{OD}{tan60°}$=$\frac{2\sqrt{3}}{3}$,
∴S阴影=S△ODE-S扇形=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$-$\frac{30π×{2}^{2}}{360}$=$\frac{2\sqrt{3}-π}{3}$.
点评 此题考查了切线的判定以及扇形面积的求解.注意准确作出辅助线是解此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
7.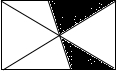 小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )
小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )
 小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )
小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
8.某工厂现在平均每天比原计划多生产50台机器,现在生产800台所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
| A. | $\frac{800}{x+50}$=$\frac{600}{x}$ | B. | $\frac{800}{x-50}$=$\frac{600}{x}$ | C. | $\frac{800}{x}$=$\frac{600}{x+50}$ | D. | $\frac{800}{x}$=$\frac{600}{x-50}$ |
5.已知点P(x,y)的坐标满足|x|=3,$\sqrt{y}$=2,且xy<0,则点P的坐标是( )
| A. | (3,-2) | B. | (-3,2) | C. | (3,-4) | D. | (-3,4) |
12.下列运算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\root{3}{4}$=2 | ||
| C. | (x+2y)2=x2+2xy+4y2 | D. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ |
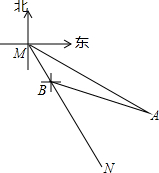 如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)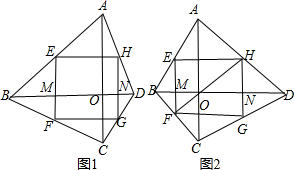
 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AN=$\frac{1}{2}$AB,AN∥CM.