题目内容
已知等腰三角形其中两边的长分别是8和6，第三边的长是一元二次方程x2-16x+60=0的一个实数根，则该三角形的周长是（ ）
| A、20 | B、24 |
| C、24或20 | D、无法确定 |
考点：等腰三角形的性质,解一元二次方程-因式分解法,三角形三边关系
专题：分类讨论
分析：求出方程的解得到x的值，利用三角形的三边关系判断即可得到结果．
解答：解：x2-16x+60=0，
因式分解得：（x-6）（x-10）=0，
解得：x=6或x=10，
当x=6时，三角形三边长为6，6，8；当x=10，三角形三边长为6，8，10，
则周长为20或24．
故选C．
因式分解得：（x-6）（x-10）=0，
解得：x=6或x=10，
当x=6时，三角形三边长为6，6，8；当x=10，三角形三边长为6，8，10，
则周长为20或24．
故选C．
点评：此题考查了解一元二次方程-因式分解法，利用此方法解方程时，首先将方程右边化为0，左边化为积的形式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
练习册系列答案
相关题目
已知⊙O的半径为7cm，OA=5cm，那么点A与⊙O的位置关系是（ ）
| A、在⊙O内 | B、在⊙O上 |
| C、在⊙O外 | D、不能确定 |
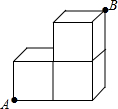如图是由三个棱长均为1的正方体箱子堆积而成的几何体，在底端的顶点A处有一只蚂蚁，它想吃到顶端的顶点B处的食物，则它沿该几何体表面爬行的最短路程等于（ ）数轴上到原点的距离等于1的点所表示的数是（ ）
| A、±1 | B、0 | C、1 | D、-1 |
小明从正面观察下图所示的两个物体，看到的是（ ）A、 |
B、 |
C、 |
D、 |
如图所示，在等腰△ABC中，AB=AC，且△ABC的周长为22cm，过腰AB的中点D作AB的垂线，交另一腰AC于E，连接BE，若△BCE的周长是14cm，则BC=