题目内容
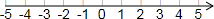 我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题:
我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题:(1)数轴上点A、点B分别是数-1、3对应的点,则点A与点B之间的距离为
(2)再选几个点试试,猜想:若点A、点B分别是数a、b对应的点,则点A与点B之间的距离为
(3)若数轴上点A对应的数为a,且|a-2|+|a-1|=12,且点A对应的数为
(4)继续利用绝对值的几何意义,探索|x-12|+|x+5|的最小值是
(5)已知数x,y满足|x+7|+|1-x|=19-|y-10|-|1+y|,则x+y的最小值是
考点:数轴,绝对值,两点间的距离
专题:
分析:(1)用3减去-1即可得到点A、点B间的距离;
(2)若点A、点B分别是有理数a、b对应的点,则点A、点B间的距离用两数之差的绝对值表示;
(3)可以把|a-2|+|a-1|=12理解为表示点A到2对应点和1对应的点的距离之和为12,而1与2对应的点表示的距离为12,则点A对应的实数为-4.5或7.5;
(4)根据线段上的点与线段两端点的距离的和最小,可得答案.
(5)先移项可得|x+7|+|1-x|+|y-10|+|1+y|=19,根据线段上的点与线段两端点的距离的和最小,可得答案.
(2)若点A、点B分别是有理数a、b对应的点,则点A、点B间的距离用两数之差的绝对值表示;
(3)可以把|a-2|+|a-1|=12理解为表示点A到2对应点和1对应的点的距离之和为12,而1与2对应的点表示的距离为12,则点A对应的实数为-4.5或7.5;
(4)根据线段上的点与线段两端点的距离的和最小,可得答案.
(5)先移项可得|x+7|+|1-x|+|y-10|+|1+y|=19,根据线段上的点与线段两端点的距离的和最小,可得答案.
解答:解:(1)点A、点B间的距离=3-(-1)=4;
(2)若点A、点B分别是有理数a、b对应的点,则点A、点B间的距离为a-b(a>b)或b-a(a<b),即|b-a|;
(3)|a-2|+|a-1|=12表示点A到2对应点和1对应的点的距离之和为12,而1与2对应的点表示的距离为12,则点A对应的实数为-4.5或7.5;
(4)说出|x-12|+|x+5|表示的几何意义 数轴上点x与12的距离与点x与-5距离的和,利用数轴及绝对值的几何意义写出该式能取得的最小值是17,
(5)原式变形为:|x+7|+|1-x|+|y-10|+|1+y|=19,
所以,要使等式满足,可得:-7≤x≤1,-1≤y≤10,
所以x+y的最小值是-8,最大值是11;
故答案为:4;|b-a|;-4.5或7.5;17;-8;11
(2)若点A、点B分别是有理数a、b对应的点,则点A、点B间的距离为a-b(a>b)或b-a(a<b),即|b-a|;
(3)|a-2|+|a-1|=12表示点A到2对应点和1对应的点的距离之和为12,而1与2对应的点表示的距离为12,则点A对应的实数为-4.5或7.5;
(4)说出|x-12|+|x+5|表示的几何意义 数轴上点x与12的距离与点x与-5距离的和,利用数轴及绝对值的几何意义写出该式能取得的最小值是17,
(5)原式变形为:|x+7|+|1-x|+|y-10|+|1+y|=19,
所以,要使等式满足,可得:-7≤x≤1,-1≤y≤10,
所以x+y的最小值是-8,最大值是11;
故答案为:4;|b-a|;-4.5或7.5;17;-8;11
点评:本题考查了数轴:数轴有三要素(原点、正方向和单位长度);原点左边的点表示负数,右边的点表示数为正数;左边点表示的数比右边点表示的数要小.也考查了绝对值.

练习册系列答案
相关题目
已知⊙O的半径为7cm,OA=5cm,那么点A与⊙O的位置关系是( )
| A、在⊙O内 | B、在⊙O上 |
| C、在⊙O外 | D、不能确定 |
 有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.
有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.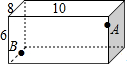 如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.
如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.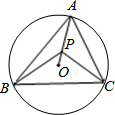 如图,⊙O是△ABC的外接圆,∠BAC=55°,点P在半径AO上(不与A,O重合),则∠BPC可能为
如图,⊙O是△ABC的外接圆,∠BAC=55°,点P在半径AO上(不与A,O重合),则∠BPC可能为 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,连接EF,EF与AD交于G
如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,连接EF,EF与AD交于G