题目内容
如果十边形的各个内角都相等，那么它的内角和是 ，它的每一个外角是 ．
考点：多边形内角与外角
专题：
分析：根据多边形的内角和计算公式（n-2）×180°进行计算，可求十边形的内角和；根据多边形的外角和是360度，除以10即可求得每一个外角．
解答：解：十边形的内角和等于：（10-2）×180°=1440°，
它的一个内角是：360°÷10=36°．
故它的内角和是1440°，它的每一个外角是36°．
故答案为：1440°，36°．
它的一个内角是：360°÷10=36°．
故它的内角和是1440°，它的每一个外角是36°．
故答案为：1440°，36°．
点评：本题主要考查了多边形的内角和定理以及多边形的外角和定理．注意多边形的外角和不随边数的变化而变化，因而把求多边形内角的计算转化为外角的计算，可以使计算简便．
练习册系列答案
名校课堂系列答案
相关题目
计算（a3b）2的结果是（ ）
| A、a6b |
| B、a5b2 |
| C、a6b2 |
| D、a3b2 |
实数a、b在数轴上的位置如图所示，那么化简|a-b|-| b2 |
| A、a-2b | B、-a |
| C、a | D、-2a+b |
分式
中的x、y的值都变为原来的3倍，则此分式的值为（ ）
| xy |
| x+y |
| A、不变 | ||
B、是原来的
| ||
C、是原来的
| ||
| D、是原来的3倍 |
已知⊙O的半径为7cm，OA=5cm，那么点A与⊙O的位置关系是（ ）
| A、在⊙O内 | B、在⊙O上 |
| C、在⊙O外 | D、不能确定 |
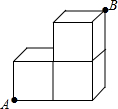如图是由三个棱长均为1的正方体箱子堆积而成的几何体，在底端的顶点A处有一只蚂蚁，它想吃到顶端的顶点B处的食物，则它沿该几何体表面爬行的最短路程等于（ ）