题目内容
过一个正多边形的某个顶点的所有对角线，将这个正多边形分成了4个三角形，则这个正多边形的每一个内角的度数是（ ）
| A、120° | B、90° |
| C、60° | D、30° |
考点：多边形的对角线,多边形内角与外角
专题：
分析：先由经过n边形的一个顶点的所有对角线把多边形分成（n-2）个三角形，求出n的值，得到这个正多边形的边数，再根据多边形的外角和为360°求出每一个外角的度数，进而根据多边形的每一个内角与其相邻的外角互为邻补角即可求解．
解答：解：∵过一个正多边形的某个顶点的所有对角线，将这个正多边形分成了4个三角形，
∴此多边形为正六边形，
∵多边形外角和为360°，
∴这个正多边形的每一个外角的度数是：360°÷6=60°，
∴这个正多边形的每一个内角的度数：180°-60°=120°，
故选：A．
∴此多边形为正六边形，
∵多边形外角和为360°，
∴这个正多边形的每一个外角的度数是：360°÷6=60°，
∴这个正多边形的每一个内角的度数：180°-60°=120°，
故选：A．
点评：本题考查了多边形的对角线：n边形从一个顶点出发可引出（n-3）条对角线，这（n-3）条对角线把n边形分成（n-2）个三角形．也考查了多边形的外角和定理以及多边形内角与外角的关系．
练习册系列答案
相关题目
实数a、b在数轴上的位置如图所示，那么化简|a-b|-| b2 |
| A、a-2b | B、-a |
| C、a | D、-2a+b |
已知⊙O的半径为7cm，OA=5cm，那么点A与⊙O的位置关系是（ ）
| A、在⊙O内 | B、在⊙O上 |
| C、在⊙O外 | D、不能确定 |
已知二次函数y=-x2+bx+c，当x＞1时，y的值随x值的增大而减小，则实数b的取值范围是（ ）
| A、b≥-2 | B、b≤-2 |
| C、b≥2 | D、b≤2 |
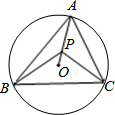如图，⊙O是△ABC的外接圆，∠BAC=55°，点P在半径AO上（不与A，O重合），则∠BPC可能为
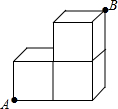如图是由三个棱长均为1的正方体箱子堆积而成的几何体，在底端的顶点A处有一只蚂蚁，它想吃到顶端的顶点B处的食物，则它沿该几何体表面爬行的最短路程等于（ ）
如图所示，在等腰△ABC中，AB=AC，且△ABC的周长为22cm，过腰AB的中点D作AB的垂线，交另一腰AC于E，连接BE，若△BCE的周长是14cm，则BC=