题目内容
13. 如图,AC∥ED,AB∥FD,∠A=64°,则∠EDF的度数为64°.
如图,AC∥ED,AB∥FD,∠A=64°,则∠EDF的度数为64°.
分析 首先根据两直线平行,同位角相等求出∠DEB的度数,再根据两直线平行,内错角相等求出∠EDF的度数.
解答 解:∵AC∥DE,∠A=64°,
∴∠DEB=∠A=64°(两直线平行,同位角相等).
∵DF∥AB,
∴∠EDF=∠DEB=64°(两直线平行,内错角相等).
故答案为64°.
点评 本题考查了平行线的性质,解决本题的关键是熟记平行线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:
某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:
(1)根据图象完成下表:
(2)售价为560元时,日销售量为750件.
(3)如果该商场要求日销售量为1110件,该商品应降价500元.
(4)设该商品的售价为x(x≤560)元,日销售量为y件,求y与x之间的关系式.
 某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:
某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:(1)根据图象完成下表:
| 降价/元 | 5 | 10 | 15 | 20 |
| 日销售量/件 | 780 | 810 | 840 | 870 |
(3)如果该商场要求日销售量为1110件,该商品应降价500元.
(4)设该商品的售价为x(x≤560)元,日销售量为y件,求y与x之间的关系式.
5.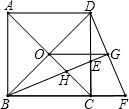 如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )
如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )
 如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )
如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )| A. | △BCE≌△DCF | B. | OG∥AD | C. | BH=GH | D. | OG=$\frac{1}{2}$BD |
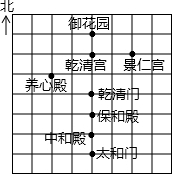 如图所示的是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且表示保和殿的点的坐标为(1,-4),表示景仁宫的点的坐标为(3,-1),则表示养心殿的点的坐标是(-1,-2).
如图所示的是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且表示保和殿的点的坐标为(1,-4),表示景仁宫的点的坐标为(3,-1),则表示养心殿的点的坐标是(-1,-2). 如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.
如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$. 在如图所示的4×4方格中,每个小方格的边长都为1
在如图所示的4×4方格中,每个小方格的边长都为1