题目内容
11.如图,⊙O的半径OA⊥OC,点D在$\widehat{AC}$上,且$\widehat{AD}$=2$\widehat{CD}$,OA=4.
(1)∠COD=30°;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)
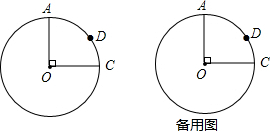
分析 (1)根据垂直的定义得到∠AOC=90°,由已知条件得到∠AOD=2∠COD,即可得到结论;
(2)连结OD、AD,如图1所示:由(1)知∠AOD=2∠COD=2×30°=60°,推出△AOD为等边三角形,根据等边三角形的性质得到;
(3)过点D作DE⊥OC,交⊙O于点E,连结AE,交OC于点P,则此时,AP+PD的值最小,延长AO交⊙O于点B,连结BE,得到AP+PD最小值=AP+PE=AE,根据圆周角定理得到∠AED=$\frac{1}{2}$∠AOD=30°,根据平行线的性质得到∠OAE=∠AED=30°,由于AB为直径,得到△ABE为直角三角形,解直角三角形即可得到结论.
解答 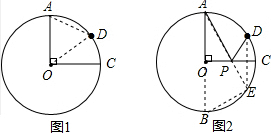 解:(1)∵OA⊥OC,
解:(1)∵OA⊥OC,
∴∠AOC=90°,
∵$\widehat{AD}$=2$\widehat{CD}$,
∴∠AOD=2∠COD,
∴∠COD=$\frac{1}{3}$∠AOC=30°,
故答案为:30;
(2)连结OD、AD,如图1所示:
由(1)知∠AOD=2∠COD=2×30°=60°,
∵OA=OD,
∴△AOD为等边三角形,
∴AD=OA=4;
(3)过点D作DE⊥OC,交⊙O于点E,连结AE,交OC于点P,则此时,AP+PD的值最小,
延长AO交⊙O于点B,连结BE,如图2所示:
∵根据圆的对称性,点E是点D关于OC的对称点,
OC是DE的垂直平分线,
即PD=PE,
∴AP+PD最小值=AP+PE=AE,
∵∠AED=$\frac{1}{2}$∠AOD=30°,
又∵OA⊥OC,DE⊥OC,
∴OA∥DE,
∴∠OAE=∠AED=30°,
∵AB为直径,
∴△ABE为直角三角形,由$\frac{AE}{AB}$=cos∠BAE,AE=AB•cos30°=2×4×$\frac{{\sqrt{3}}}{2}$=$4\sqrt{3}$,
即AP+PD=$4\sqrt{3}$,
点评 本题考查了圆心角,弧、弦的关系,轴对称的性质,勾股定理,垂径定理,正确的作出辅助线是解题的关键.

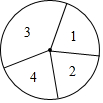 如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )
如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
 如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.
如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.
 如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则AF的长为4.
如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则AF的长为4.