题目内容
10．
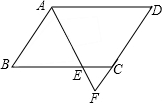如图，在?ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，已知AB=6，AD=9，∠F=64°，求FC的长和∠B的度数．
分析 利用平行四边形的性质以及平行线的性质得出∠BAF=∠DAF=∠F=64°，证出DF=AD=9，求出FC=3，由三角形内角和定理求出∠B的度数即可．
解答 解：∵四边形ABCD是平行四边形，
∴BC=AD=9，AD∥BC，AB∥DE，CD=AB=6，
∴∠DAF=∠BEA，∠BAF=∠F=64°，
∵AF平分∠BAD，
∴∠BAF=∠DAF=∠F=64°，
∴DF=AD=9，
∴FC=DF-CD=3，
∵∠BAF=∠BEA=64°，
∴∠B=180°-2×64°=52°．
点评 此题主要考查了平行四边形的性质以及平行线的性质等知识，熟练应用平行四边形的性质得出是解题关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，矩形的两条对角线夹角为60°，一条短边为3，则矩形的长边长为3$\sqrt{3}$．
18．
某商场销售某种商品，原价560元，随着不同幅度的降价（元），日销售量（件）发生相应变化，关系如图所示：
（1）根据图象完成下表：
（2）售价为560元时，日销售量为750件．
（3）如果该商场要求日销售量为1110件，该商品应降价500元．
（4）设该商品的售价为x（x≤560）元，日销售量为y件，求y与x之间的关系式．
某商场销售某种商品，原价560元，随着不同幅度的降价（元），日销售量（件）发生相应变化，关系如图所示：（1）根据图象完成下表：
| 降价/元 | 5 | 10 | 15 | 20 |
| 日销售量/件 | 780 | 810 | 840 | 870 |
（3）如果该商场要求日销售量为1110件，该商品应降价500元．
（4）设该商品的售价为x（x≤560）元，日销售量为y件，求y与x之间的关系式．
5．
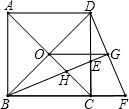如图，O为正方形ABCD对角线BD的中点，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，连接OG、OC，OC交BG于点H．下面四个结论中不正确的是（ ）
如图，O为正方形ABCD对角线BD的中点，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，连接OG、OC，OC交BG于点H．下面四个结论中不正确的是（ ）| A． | △BCE≌△DCF | B． | OG∥AD | C． | BH=GH | D． | OG=$\frac{1}{2}$BD |
20．
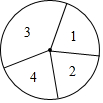如图是一个转盘，扇形1，2，3的圆心角分别是60°，70°，150°，任意转动转盘，指针指向扇形4的概率是（ ）
如图是一个转盘，扇形1，2，3的圆心角分别是60°，70°，150°，任意转动转盘，指针指向扇形4的概率是（ ）| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{1}{3}$ | D． | $\frac{4}{9}$ |