题目内容
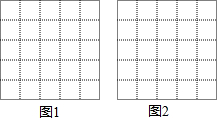
11.如图,正方形网格中的每个小正方形的边长都是1,每个顶点叫作格点.(1)在图1中以格点为顶点画一个面积为5的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为1,3,$\sqrt{10}$,并求该三角形的面积.
分析 (1)根据题意得出正方形的边长为$\sqrt{5}$,利用勾股定理作图可得;
(2)利用勾股定理作出$\sqrt{10}$的线段可得该直角三角形,继而可得三角形的面积.
解答 解:(1)如图1所示;
(2)如图2所示,该三角形面积S=$\frac{1}{2}$×1×3=$\frac{3}{2}$.
点评 本题主要考查作图-应用与设计作图,熟练掌握平方根的定义和勾股定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如果x+y=4,那么代数式$\frac{2x}{{x}^{2}-{y}^{2}}$-$\frac{2y}{{x}^{2}-{y}^{2}}$的值是( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
19.一个不透明的盒子中装有2个白球,3个红球和5个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出1个球,摸到红球的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
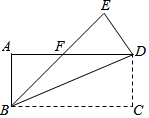 如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.
如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.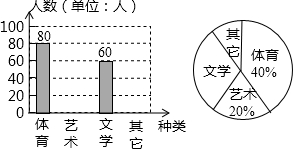 为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题: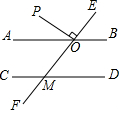 如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O,若∠AOP=30°,求∠EMD的度数.
如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O,若∠AOP=30°,求∠EMD的度数. 如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.
如图,矩形的两条对角线夹角为60°,一条短边为3,则矩形的长边长为3$\sqrt{3}$.