题目内容
6.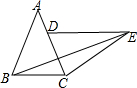 △ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.
△ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.
分析 先由旋转得到∠EDC=∠ABC=∠ACB=∠DCE,再利用三角形的外角计算出∠EBC,再求出∠ABC,即可.
解答 解:∵∠ABC=∠ACB,
由旋转得,∠EDC=∠ABC=∠ACB=∠DCE,
∵∠DEB=30°,
∵∠CDE+∠DEB=∠EBC+∠ACB,
∴∠EBC=∠DEC=30°,
∴∠BCE=180°-∠EBC-∠BEC=180°-30°-18°=132°,
∴∠ABC=∠ACB=$\frac{1}{2}$∠BCE=66°,
∴∠ABE=∠ABC-∠EBC=66°-30°=36°,
故答案为36°.
点评 此题是旋转的性质题,主要考查了旋转的性质,三角形外角的性质,等腰三角形的性质,解本题的关键是用三角形的外角求出∠RBC.

练习册系列答案
相关题目
14.圆锥体是由下列哪个图形绕自身的对称轴旋转一周得到的( )
| A. | 正方形 | B. | 等腰三角形 | C. | 圆 | D. | 等腰梯形 |
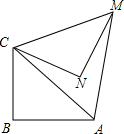 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.