题目内容
2.当a+b=$\frac{3}{2}$,ab=$\frac{1}{2}$时,代数式4a2b+4ab2的值是3.分析 首先将原式提取公因式进而将已知代入求出即可.
解答 解:∵a+b=$\frac{3}{2}$,ab=$\frac{1}{2}$,
∴4a2b+4ab2=4ab(a+b)=4×$\frac{1}{2}$×$\frac{3}{2}$=3.
故答案为:3.
点评 此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
12.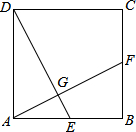 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
17.下面几组数:①7,8,9;②12,9,15;③a2,a2+1,a2+2;④m2+n2,m2-n2,2mn(m、n均为正整数,m>n),其中能组成直角三角形的三边长的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
7.如图,∠1和∠2是对顶角的图形是( )


| A. | 甲 | B. | 丙 | C. | 丁 | D. | 乙 |
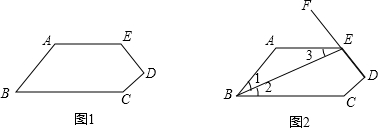
11.如图1,在五边形ABCDE中,AE∥BC,∠A=∠C.
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)延长DE至F,连接BE,如图2,若∠1=∠3,∠AEF=2∠2,求证:∠AED=∠C.
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)延长DE至F,连接BE,如图2,若∠1=∠3,∠AEF=2∠2,求证:∠AED=∠C.

12.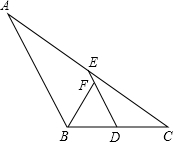 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )| A. | 3 | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
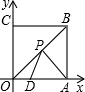 如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$.
如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$. 将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.
将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.