题目内容
17.下面几组数:①7,8,9;②12,9,15;③a2,a2+1,a2+2;④m2+n2,m2-n2,2mn(m、n均为正整数,m>n),其中能组成直角三角形的三边长的是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
分析 根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.
解答 解:①72+82≠92,故不是直角三角形;
②92+122=152,故是直角三角形;
③(a2)2+(a2+1)2≠(a2+2)2,故不是直角三角形;
④(2mn)2+(m2-n2)2=(m2+n2)2,故是直角三角形;
故选:D.
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
相关题目
 如图,已知△ABC
如图,已知△ABC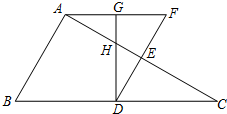 如图,△ABC中,BC=2AB,点D、E分别是BC、AC的中点,过点A作AF∥BC交线段DE的延长线于点F,取AF的中点G,联结DG,GD与AE交于点H.
如图,△ABC中,BC=2AB,点D、E分别是BC、AC的中点,过点A作AF∥BC交线段DE的延长线于点F,取AF的中点G,联结DG,GD与AE交于点H.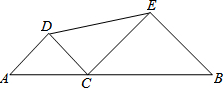 如图,线段AB的长为10,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角△ACD和△BCE,那么DE长的最小值是5.
如图,线段AB的长为10,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角△ACD和△BCE,那么DE长的最小值是5.