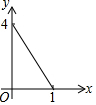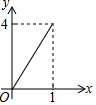题目内容
11.当实数x的取值使得$\sqrt{x-2}$有意义时,对于函数y=4x+1,下列说法正确的是( )| A. | 图象是一条直线 | B. | y有最大值 | ||
| C. | y有最小值 | D. | y既没有最大值也没有最小值 |
分析 先根据二次根式有意义的条件求出x的取值范围,再把函数y=4x+1化为x=$\frac{y-1}{4}$的形式,求出y的取值范围即可.
解答 解:∵$\sqrt{x-2}$有意义,
∴x-2≥0,即x≥2,
∵函数y=4x+1化为x=$\frac{y-1}{4}$,
∴$\frac{y-1}{4}$≥2,
解得y≥9,
∴y有最小值9.
故选C.
点评 本题考查的是一次函数的性质及二次根式有意义的条件,先根据题意求出x的取值范围是解答此题的关键.

练习册系列答案
相关题目
20.揭西县是全国著名的侨乡,拥有海外华侨、华人及港、澳、台同胞共608000人,这一数据用科学记数法表示为( )
| A. | 0.608×106 | B. | 6.08×105 | C. | 6.08×106 | D. | 60.8×104 |
1.若点(a,b)在一次函数y=2x-3的图象上,则代数式8a-4b+2的值是( )
| A. | -10 | B. | -6 | C. | 10 | D. | 14 |
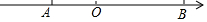 如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.
如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.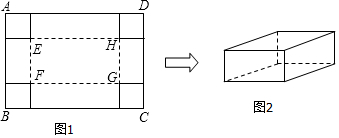
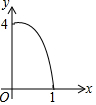
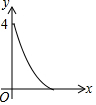
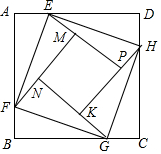 如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )