题目内容
16.商店购进一种商品进行销售,进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映:调整价格时,售价每涨1元每月要少卖10件,售价每下降1元每月要多卖20件,为了获得更大的利润,现将商品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月商品销量为y(件),月利润为w(元).(1)直接写出y与x之间的函数关系式;
(2)当销售价格是多少时才能使月利润最大?最大月利润是多少?
分析 (1)直接根据题意售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件,进而得出等量关系;
(2)利用每件利润×销量=总利润,进而利用配方法求出即可.
解答 解:(1)由题意可得:y=$\left\{\begin{array}{l}{300-10x(0≤x≤30)}\\{300-20x(-20≤x<0)}\end{array}\right.$;
(2)由题意可得:w=$\left\{\begin{array}{l}{(20+x)(300-10x)(0≤x≤30)}\\{(20+x)(300-20x)(-20≤x<0)}\end{array}\right.$,
化简得:w=$\left\{\begin{array}{l}{-10{x}^{2}+100x+6000(0≤x≤30)}\\{-20{x}^{2}-100x+6000(-20≤x<0)}\end{array}\right.$,
即w=$\left\{\begin{array}{l}{-10(x-5)^{2}+6250(0≤x≤30)}\\{-20(x+\frac{5}{2})^{2}+6125(-20≤x<0)}\end{array}\right.$,
由题意可知x应取整数,故当x=-2或x=-3时,w<6125,
x=5时,W=6250,
故当销售价格为65元时,利润最大,最大月利润为6250元;
点评 此题主要考查了二次函数的应用以及配方法求二次函数最值等知识,利用x的取值范围分情况得出函数解析式是解题关键.

练习册系列答案
相关题目
11.当实数x的取值使得$\sqrt{x-2}$有意义时,对于函数y=4x+1,下列说法正确的是( )
| A. | 图象是一条直线 | B. | y有最大值 | ||
| C. | y有最小值 | D. | y既没有最大值也没有最小值 |
5.8的平方根是( )
| A. | 2 | B. | ±2 | C. | 2$\sqrt{2}$ | D. | $±2\sqrt{2}$ |
 如图,在平面内直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC,点E是y轴上任意一点,记点E为(0,n).
如图,在平面内直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC,点E是y轴上任意一点,记点E为(0,n).
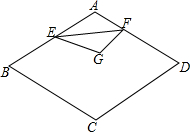 如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$.
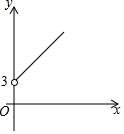
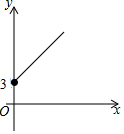
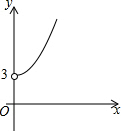
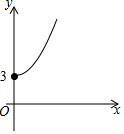
如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$. 如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )
如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )