题目内容
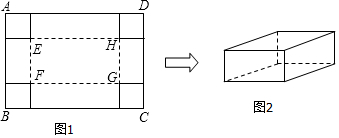
19.在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.
分析 (1)一边长为90cm,则另一边长为40cm,列出侧面积的函数解析式,配方可得最值;
(2)由EH:EF=7:2,设EF=2m、EH=7m,根据侧面积与底面积之比为9:7建立方程,可得m=x,由矩形纸板面积得出x的值.
解答 解:(1)∵矩形纸板ABCD的一边长为90cm,
∴矩形纸板的另一边长为3600÷90=40(cm),
则S侧=2[x(90-2x)+x(40-2x)]=-8x2+260x,
=-8(x-$\frac{65}{4}$)2+$\frac{4225}{2}$.
∵-8<0,
∴当x=$\frac{65}{4}$时,S侧最大=$\frac{4225}{2}$.
(2)设EF=2m,则EH=7m,
则侧面积为2(7mx+2mx)=18mx,底面积为7m•2m=14m2,
由题意,得18mx:14m2=9:7,
∴m=x.
则AD=7x+2x=9x,AB=2x+2x=4x
由4x•9x=3600,且x>0,
∴x=10.
点评 本题主要考查二次函数的应用,根据矩形的面积公式列出面积的函数表达式或方程是解题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
9.一列长150米的火车,以每秒15米的速度通过750米的隧道,从火车进入隧道口算起,这列火车完全通过隧道所需时间是( )
| A. | 70秒 | B. | 60秒 | C. | 50秒 | D. | 40秒 |
11.当实数x的取值使得$\sqrt{x-2}$有意义时,对于函数y=4x+1,下列说法正确的是( )
| A. | 图象是一条直线 | B. | y有最大值 | ||
| C. | y有最小值 | D. | y既没有最大值也没有最小值 |
 如图,在平面内直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC,点E是y轴上任意一点,记点E为(0,n).
如图,在平面内直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC,点E是y轴上任意一点,记点E为(0,n).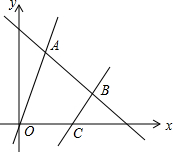 如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.
如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.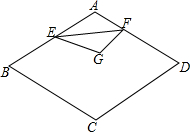 如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$.
如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$.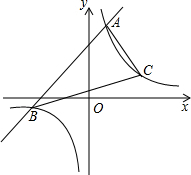 如图,已知一次函数y1=x+b(b>0)的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
如图,已知一次函数y1=x+b(b>0)的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.