题目内容
6.“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
分析 (1)设平均增长率为x,根据1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆列出方程,再求解即可;
(2)设购进A型车x辆,则购进B型车100-x辆,根据不超过70000元的资金再购进A,B两种规格的自行车100辆,列出不等式,求出x的取值范围,然后求出利润W的表达式,根据一次函数的性质求解即可.
解答 解:(1)设平均增长率为x,根据题意得:
640(x+1)2=1000,
解得:x=0.25=25%或x=-2.25(不合题意,舍去),
则四月份的销量为:1000(1+25%)=1250辆,
答:该公司4月份在深圳市新投放共享单车1250辆;
(2)设购进A型车x辆,则购进B型车100-x辆,
根据题意得:500x+1000(100-x)≤70000,
解得:x≥60.
利润W=(700-500)x+(1300-1000)(100-x)=200x+300(100-x)=-100x+30000,
∵-100<0,
∴W随着x的增大而减小.
当x=60时,利润最大=-100×60+30000=24000,
答:为使利润最大,该商城应购进60辆A型车和40辆B型车.
点评 本题考查了一元二次方程、一元一次不等式和一次函数的应用,解题关键是读懂题意,根据题意列出方程或不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列说法中错误的是( )
| A. | 如果整数a是整数b的倍数,那么b是a的因数 | |
| B. | 一个合数至少有3个因数 | |
| C. | 在正整数中,除2外所有的偶数都是合数 | |
| D. | 在正整数中,除了素数都是合数 |
1. 如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )
如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )
 如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )
如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )| A. | S1<S3<S2 | B. | S1<S2<S3 | C. | S2<S1<S3 | D. | S3<S1<S2 |
11.当实数x的取值使得$\sqrt{x-2}$有意义时,对于函数y=4x+1,下列说法正确的是( )
| A. | 图象是一条直线 | B. | y有最大值 | ||
| C. | y有最小值 | D. | y既没有最大值也没有最小值 |
15.4的绝对值可表示为( )
| A. | -4 | B. | |4| | C. | $\sqrt{4}$ | D. | $\frac{1}{4}$ |
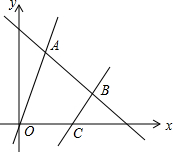 如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.
如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.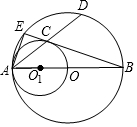 如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E.
如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E. 如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )
如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )