题目内容
3.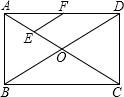 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm.
分析 先求出矩形的对角线AC,根据中位线定理可得出EF,继而可得出△AEF的周长.
解答 解:在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{D}^{2}}$=20cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=$\frac{1}{2}$OD=$\frac{1}{4}$BD=4cm,
∵AF=$\frac{1}{2}$AD=$\frac{1}{2}$BC=6cm,AE=$\frac{1}{2}$AO=$\frac{1}{4}$AC=5cm,
∴△AEF的周长=AE+AF+EF=5+6+4=15(cm).
故答案是:15cm.
点评 本题考查了三角形的中位线定理、勾股定理及矩形的性质,解答本题需要我们熟练掌握三角形中位线的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°40′,则∠B的度数为65°40′.
如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°40′,则∠B的度数为65°40′.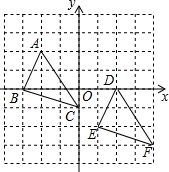 如图,三角形ABC是由三角形DEF经过某种变换得到的,观察对应点A与D,B与E,C与F的坐标变化,说明三角形ABC是由三角形DEF经过怎样的变换得到的.
如图,三角形ABC是由三角形DEF经过某种变换得到的,观察对应点A与D,B与E,C与F的坐标变化,说明三角形ABC是由三角形DEF经过怎样的变换得到的. 如图,AB∥CD,EF交AB于点E,交CD于点F,FG,EG分别平分∠CFE和∠AEF,FH,EH分别平分∠DFE和∠BEF,求证:四边形EGFH是矩形.
如图,AB∥CD,EF交AB于点E,交CD于点F,FG,EG分别平分∠CFE和∠AEF,FH,EH分别平分∠DFE和∠BEF,求证:四边形EGFH是矩形. 如图,平面上六个点A,B,C,D,E,F构成一个封闭的折线图形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图,平面上六个点A,B,C,D,E,F构成一个封闭的折线图形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.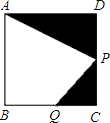 已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由.
已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由.