题目内容
15.已知y+m与x-n成正比例(其中m、n是常数).给出下列结论:①若m>0,n>0,则y关于x的函数图象不经过第二象限;②若y关于x又成正比例,则y关于x的函数解析式可表达为y=$\frac{m}{n}$x;③y关于x的函数图象必经过点(n,-m).其中正确的是( )| A. | ③ | B. | ①② | C. | ②③ | D. | ①②③ |
分析 根据题意可以设出y+m与x-n的关系式,从而可以得到y关于x的函数关系式,然后根据①②③给出的信息进行讨论其是否正确即可解答本题.
解答 解:∵y+m与x-n成正比例(其中m、n是常数),
∴设y+m=k(x-n)
则y=kx-kn-m,
当k>0,m>0,n>0,y关于x的函数图象第一、三、四象限,
当k<0,m>0,n>0,y关于x的函数图象经过第一、二、四象限或第二、三、四象限,
故①错误;
若y关于x又成正比例,则-kn-m=0,得k=$-\frac{m}{n}$,则y=$-\frac{m}{n}x$,故②错误;
将x=n,代入y=kx-kn-m,得y=-m,故y关于x的函数图象必经过点(n,-m),故③正确;
故选A.
点评 本题考查一次函数的性质,解题的关键是能根据题意设出相应的函数关系式,根据题目提供的信息灵活转化,判断其是否争正确.

练习册系列答案
相关题目
20.已知抛物线y=x2-2mx+m2+m+2与x轴的交点为(a,0),(b,0),则(a-1)2+(b-1)2的最小值是( )
| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
14.国庆期间,某商店推出全店打8折的优惠活动,持贵宾卡的客户还可在8折的基础上再打9折.某人持贵宾卡买了一件商品共花了a元,则该商品的标价是( )
| A. | $\frac{17}{20}$a元 | B. | $\frac{20}{17}$a元 | C. | $\frac{18}{25}$a元 | D. | $\frac{25}{18}$a元 |
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=35°,求∠2的度数.
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=35°,求∠2的度数.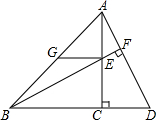 已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.
已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.