题目内容
7．已知a2+a-1=0，求下列各式的值．（1）2a2+2a
（2）a3+2a2+2014．
分析 读题先观察含有字母部分的关系：（1）2a2+2a=2（a2+a），代入即可求解；
（2）a3+2a2+2014=a3+a2+a2+2014，由a2+a-1=0可得a3+a2-a=0，代入即可求解．
解答 解：（1）∵a2+a-1=0，
∴a2+a=1，
∴2a2+2a=2（a2+a）=2×1=2．
（2）∵a2+a-1=0，
∴a3+a2-a=0，a2+a=1
∴a3+a2=a，
∴a3+2a2+2014=a3+a2+a2+2014=a+a2+2014=1+2014=2015．
点评 此题主要考察因式分解和整体代入思想的应用，观察题中含有字母部分的联系是解题的关键．
练习册系列答案
新编小学单元自测题系列答案
相关题目
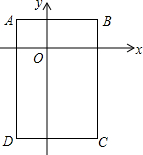如图，长方形ABCD的边与坐标轴平行，点A、C的坐标分别为（-1，1），（$\sqrt{3}$，-2$\sqrt{3}$）
如图，正方形ABCD中，E、F两点分别在BC、CD上，BE+DF=EF．求证：