题目内容
2.计算:(1)2cos45°+(2-π)0-($\frac{1}{3}$)-2;
(2)($\frac{1}{x+1}$-$\frac{1}{{x}^{2}-1}$)÷$\frac{x-2}{{x}^{2}-2x+1}$.
分析 (1)原式利用零指数幂、负整数指数幂法则,以及特殊角的三角函数值计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=2×$\frac{\sqrt{2}}{2}$+1-9=$\sqrt{2}$-8;
(2)原式=($\frac{1}{x+1}$-$\frac{1}{{x}^{2}-1}$)÷$\frac{x-2}{(x-1)^{2}}$=$\frac{x-2}{(x+1)(x-1)}$×$\frac{(x-1)^{2}}{x-2}$=$\frac{x-1}{x+1}$.
点评 此题考查了实数的运算,以及分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.在数轴上表示不等式2x-4>0的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
 “位似变化”是一种重要的几何变化,可以将图形放大或缩小,且与原图形相似.你能用位似变化解决下列问题吗?
“位似变化”是一种重要的几何变化,可以将图形放大或缩小,且与原图形相似.你能用位似变化解决下列问题吗?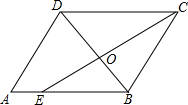 如图.在平行四边形ABCD中,CE是∠OCB的角平分线,且交AB于点E,DB与CE相交于点O,
如图.在平行四边形ABCD中,CE是∠OCB的角平分线,且交AB于点E,DB与CE相交于点O,
 如图,△ABC为等边三角形,D为BC上任一点,△ADE=60°,△ACB外角的平分线与DE边交于点E,求证:EC+CD=AB.
如图,△ABC为等边三角形,D为BC上任一点,△ADE=60°,△ACB外角的平分线与DE边交于点E,求证:EC+CD=AB. 如图,O是矩形ABCD的交点,DE∥AC,CE∥BD,DE和CE相交于点E,求证:四边形OCED是菱形.
如图,O是矩形ABCD的交点,DE∥AC,CE∥BD,DE和CE相交于点E,求证:四边形OCED是菱形.