Question

13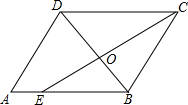．如图．在平行四边形ABCD中，CE是∠OCB的角平分线，且交AB于点E，DB与CE相交于点O，
（1）找出图中的相似三角形，并给出证明；
（2）若AB=7，BC=5，则求$\frac{OB}{OD}$的值．

Answer 1

分析 （1）由ABCD是平行四边形，得到DC∥EB，由相似三角形的判定即可得到结论；
（2）由DC∥EB，推出∠DCE=∠CEB，由∠DCE=∠ECB，得到∠ECB=∠CEB，根据等腰三角形的判定可得BE=BC=5，根据相似三角形的性质即可求得结论．

解答 （1）答：△COD∽△EOB，
证明：∵ABCD是平行四边形，
∴DC∥EB，
∴△COD∽△EOB；
（2）解：∵四边形ABCD是平行四边形，
∴DC=AB=7，DC∥EB，
∴∠DCE=∠CEB，
∵∠DCE=∠ECB，
∴∠ECB=∠CEB，
∴BE=BC=5，由（1）知：△COD∽△EOB，
∴$\frac{OB}{OD}=\frac{BE}{DC}=\frac{5}{7}$．

点评 本题主要考查了相似三角形的判定和性质，平行四边形的性质，等腰三角形的判定与性质，熟练掌握相似三角形的判定和性质是解决问题的关键．