题目内容
9. 如图,在?ABCD中,∠ABC是锐角,M是AD边上一点,且BM+MC=$\frac{14}{5}$AB,BM与CD的延长线交于点E,把?ABCD沿直线CM折叠,点B恰巧与点E重合,若AB边上的一点P满足P、B、C、M在同一圆上,设BC=a,则CP=$\frac{24}{25}$a或a.(用含a的代数式表示)
如图,在?ABCD中,∠ABC是锐角,M是AD边上一点,且BM+MC=$\frac{14}{5}$AB,BM与CD的延长线交于点E,把?ABCD沿直线CM折叠,点B恰巧与点E重合,若AB边上的一点P满足P、B、C、M在同一圆上,设BC=a,则CP=$\frac{24}{25}$a或a.(用含a的代数式表示)
分析 由折叠的性质得到CM⊥BE,MB=ME,BC=CE,根据平行线的性质得到∠1=∠E根据全等三角形的性质得到S△ABM=S△DEM,AB=DE,推出S平行四边形ABCD=AB•PC,得到PC=$\frac{BM•MC}{AB}$,根据已知条件得到AB=$\frac{5}{14}$(BM+MC),得到PC=$\frac{14BM•MC}{5(BM+MC)}$,由于EC=CD+DE=AB+AB=2AB,BC=EC=a,于是得到AB=$\frac{1}{2}$a,根据完全平方公式得到a2+2BM•MC=$\frac{49}{25}$a2,于是得到结论.
解答 解:①如图,由折叠的性质得CM⊥BE,MB=ME,BC=CE,
∵AB∥CE,
∴∠1=∠E,
在△ABM与△DEM中,$\left\{\begin{array}{l}{∠1=∠E}\\{MB=ME}\\{∠2=∠3}\end{array}\right.$,
∴△ABM≌△DEM,
∴S△ABM=S△DEM,AB=DE,
∴S平行四边形ABCD=S梯形MBCD+S△ABM=S梯形MBCD+S△DEM=S△BCE=2S△BMC=2×$\frac{1}{2}$BM•MC,
∵S平行四边形ABCD=AB•PC,
∴PC=$\frac{BM•MC}{AB}$,
∵BM+MC=$\frac{14}{5}$AB,
∴AB=$\frac{5}{14}$(BM+MC),
∴PC=$\frac{14BM•MC}{5(BM+MC)}$,
∵EC=CD+DE=AB+AB=2AB,BC=EC=a,
∴AB=$\frac{1}{2}$a,
∵(BM+MC)2=BM2+2MB•CM+CM2=BC2+2BM•MC=($\frac{14}{5}$×$\frac{1}{2}$a)2=$\frac{49}{25}$a2,
∴a2+2BM•MC=$\frac{49}{25}$a2,
∴2BM•MC=$\frac{24}{25}$a2,
∴PC=$\frac{7×\frac{24}{25}{a}^{2}}{5×\frac{7}{5}a}$=$\frac{24}{25}$a.
②P,B,C,M四点共圆,∴与AB边的另一个交点与点B重合,
∴PC=a,
故答案为:$\frac{24}{25}$a或a.
点评 本题考查了折叠的性质,平行四边形的性质,全等三角形的判定和性质,圆周角定理,正确的作出图形是解题的关键.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案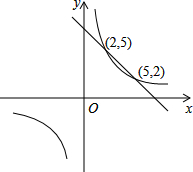 已知,一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图所示,当y1<y2时,x的取值范围是( )
已知,一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图所示,当y1<y2时,x的取值范围是( )| A. | x<2 | B. | 0<x<2或x>5 | C. | 2<x<5 | D. | x>5 |
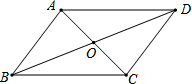 如图,?ABCD中,对角线AC、BD相交于点O,下列说法一定正确的是( )
如图,?ABCD中,对角线AC、BD相交于点O,下列说法一定正确的是( )| A. | AO=BO | B. | AC⊥BD | C. | AB=BC | D. | AB=CD |
| A. | $\sqrt{2}$ | B. | $\sqrt{24}$ | C. | $\sqrt{27}$ | D. | $\sqrt{50}$ |
| A. | 17a3b6 | B. | 8a6b12 | C. | -a3b6 | D. | 15a3b6 |
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 如图,点A、B、C、D在⊙O上,DE⊥OA,DF⊥OB,垂足分别为E,F,若∠EDF=50°,则∠C的度数为( )
如图,点A、B、C、D在⊙O上,DE⊥OA,DF⊥OB,垂足分别为E,F,若∠EDF=50°,则∠C的度数为( )| A. | 40° | B. | 50° | C. | 65° | D. | 130° |
| A. | x>0 | B. | 0<x<15 | C. | 0<x<30 | D. | 15<x<30 |



