题目内容
18.反比例函数的图象过点(2,-5),求:(1)函数y与自变量x之间的关系式,它的图象在第几象限内?y随x的减小如何变化?
(2)请画出函数图象,并判断点(-3,0),(-5,2)是否在图象上?
分析 (1)首先设y=$\frac{k}{x}$,再把点(2,-5)代入反比例函数解析式,可得k的值,再根据反比例函数的性质可得所在象限,进而可得,y随x的减小而减小;
(2)首先画出图形,再根据横纵坐标之积=k的就在此反比例函数图象上,反之则不再进行判断.
解答 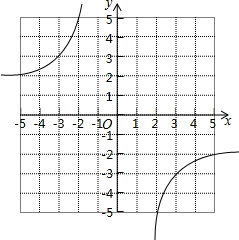 解:(1)设y=$\frac{k}{x}$,
解:(1)设y=$\frac{k}{x}$,
∵图象过点(2,-5),
∴-5=$\frac{k}{2}$,
k=-10,
∴反比例函数解析式为y=-$\frac{10}{x}$,
∵k=-10<0,
∴它的图象在第二、四象限内,y随x的减小而减小;
(2)∵-3×0=0≠-10,
∴(-3,0)不在此反比例函数图象上;
∵-5×2=-10,
∴(-5,2)在此反比例函数图象上.
点评 此题主要考查了求反比例函数解析式、反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是掌握反比例函数图象上的点横纵坐标之积=k.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
3.下列四个二次根式:①$\sqrt{8}$;②$\sqrt{18}$;③$\sqrt{\frac{3}{2}}$;④$\sqrt{12}$,能与$\sqrt{3}$合并的二次根式是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
17.若函数y=(k2-1)x2-2(k+1)x+1(k为常数)的图象与x轴没有公共点,则k的取值范围是( )
| A. | k<-1 | B. | k<0,且k≠-1 | C. | k≤-1 | D. | k=1,或k≤-1 |
 如图,AB∥EF∥DC,EG∥DB,则图中与∠EGA相等的角共有5个.
如图,AB∥EF∥DC,EG∥DB,则图中与∠EGA相等的角共有5个.