题目内容
13．
如图，AB∥EF∥DC，EG∥DB，则图中与∠EGA相等的角共有5个．
分析 由AB∥EF∥DC，EG∥DB，根据两直线平行，同位角相等与两直线平行，内错角相等，即可求得∠EGA=∠DBA，∠EGA=∠FEG，∠DBA=∠1=∠CDB，又由对顶角相等，求得∠1=∠2，则可求得答案．
解答 
解：∵AB∥EF∥DC，EG∥DB，
∴∠EGA=∠DBA，∠EGA=∠FEG，∠DBA=∠1=∠CDB，
∵∠1=∠2，
∴∠EGA=∠FEG=∠DBA=∠CDB=∠1=∠2．
∴图中与∠EGA相等的角共有5个．
故答案为：5．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等，内错角相等．
练习册系列答案
相关题目
4．
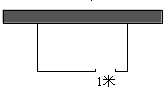如图，有一长方形鸡场，鸡场的一边靠墙（墙长18米），另三边用竹篱笆围成，竹篱笆的总长为35米，与墙平行的边留有1米宽的门（门用其它材料做成），若鸡场的面积为160平方米，则鸡场与墙垂直的边长为（ ）
如图，有一长方形鸡场，鸡场的一边靠墙（墙长18米），另三边用竹篱笆围成，竹篱笆的总长为35米，与墙平行的边留有1米宽的门（门用其它材料做成），若鸡场的面积为160平方米，则鸡场与墙垂直的边长为（ ）| A． | 7.5米 | B． | 8米 | C． | 10米 | D． | 10米或8米 |
8．合肥市某商场为做好“家电下乡”的惠民服务，决定从厂家购进甲、乙、丙三种不同型号的电视机108台，其中甲种电视机的台数是丙种的4倍，购进三种电视机的总金额不超过147000元，已知甲、乙、丙三种型号的电视机的出厂价格和售出后每台的利润如下表：
（1）求该商场至少购买丙种电视机多少台？
（2）若要求甲种电视机的台数不超过乙种电视机的台数，且使售出后所获利润最高，请设计进货方案，并求出售出后的最高利润．
| 型号 | 甲 | 乙 | 丙 |
| 出厂价（元/台） | 1000 | 1500 | 2000 |
| 每台利润（元/台） | 200 | 200 | 300 |
（2）若要求甲种电视机的台数不超过乙种电视机的台数，且使售出后所获利润最高，请设计进货方案，并求出售出后的最高利润．
5．
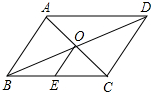如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E是边BC的中点，AB=4，则OE的长为（ ）
如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E是边BC的中点，AB=4，则OE的长为（ ）| A． | $\sqrt{2}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | 2 |
已知∠1=∠2，AC=BD，E，F，A，B在同一直线上，问∠3=∠4吗？