题目内容
17.若函数y=(k2-1)x2-2(k+1)x+1(k为常数)的图象与x轴没有公共点,则k的取值范围是( )| A. | k<-1 | B. | k<0,且k≠-1 | C. | k≤-1 | D. | k=1,或k≤-1 |
分析 分k2-1≠0与k2-1=0两种情况,根据图象与x轴没有公共点,求出k的范围即可.
解答 解:∵函数y=(k2-1)x2-2(k+1)x+1(k为常数)的图象与x轴没有公共点,
∴当k2-1≠0,即k≠1或-1时,△=4(k+1)2-4(k2-1)=4k2+8k+4-4k2+4=8k+8<0,
解得:k<-1;
当k2-1=0,即k=1时,函数y=-4x+1(舍去)或k=-1时,y=1,图象与x轴没有公共点,
综上,k的取值范围是k≤-1.
点评 此题考查了抛物线与x轴的交点,以及一次函数图象上点的坐标特征,利用了分类讨论的思想,分类讨论时注意考虑问题要全面,做到不重不漏.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
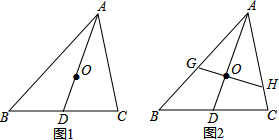
 已知∠1=∠2,AC=BD,E,F,A,B在同一直线上,问∠3=∠4吗?
已知∠1=∠2,AC=BD,E,F,A,B在同一直线上,问∠3=∠4吗?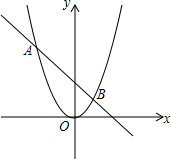 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx+c=0的解为无解.
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx+c=0的解为无解.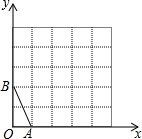 在方格纸中,每个小格的顶点称为格点,以格点的连线为边的三角形称为格点三角形,如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为(4,4)或(5,2).
在方格纸中,每个小格的顶点称为格点,以格点的连线为边的三角形称为格点三角形,如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为(4,4)或(5,2).