题目内容
16.某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元;当销售6只甲种、3只乙种圆规,可获利润39元.(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共进货甲、乙两种圆规50只并全部销售完,已知甲种圆规至少能销售30只,请判断文具店如何进货才有最大利润,并求出利润的最大值.
分析 (1)设销售甲种圆规的利润为x元/只,销售乙种圆规的利润为y元/只,根据“当销售5只甲种、1只乙种圆规,可获利润25元;当销售6只甲种、3只乙种圆规,可获利润39元”即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设文具店购进甲种圆规z只,总利润为w元,则购进乙种圆规(50-z)只,根据总利润=甲种圆规的单件利润×购进数量+乙种圆规的单件利润×购进数量即可得出w关于z的一次函数关系式,根据一次函数的性质结合z的取值范围即可解决最值问题.
解答 解:(1)设销售甲种圆规的利润为x元/只,销售乙种圆规的利润为y元/只,
根据题意得:$\left\{\begin{array}{l}{5x+y=25}\\{6x+3y=39}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$.
答:该文具店销售甲种圆规每只的利润为4元,销售乙种圆规每只的利润为5元.
(2)设文具店购进甲种圆规z只(30≤z≤50),总利润为w元,则购进乙种圆规(50-z)只,
根据题意得:w=4z+5(50-z)=-z+250,
∵-1<0,z≥30,
∴当z=30时,利润取最大值,最大值为220.
答:文具店购进甲种圆规30只、乙种圆规20只时,销售利润最大,最大利润为220元.
点评 本题考查了一次函数的应用、一次函数的性质以及二元一次方程组的应用,解题的关键是:(1)根据“当销售5只甲种、1只乙种圆规,可获利润25元;当销售6只甲种、3只乙种圆规,可获利润39元”列出关于x、y的二元一次方程组;(2)根据总利润=甲种圆规的单件利润×购进数量+乙种圆规的单件利润×购进数量找出w关于z的一次函数关系式.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案 如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4.
如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4. 如图,用小立方块搭成一个几何体,使得它的从正面与上面看到的图形如图所示.他至少需要10个小立方块,最多需要13个小立方块.
如图,用小立方块搭成一个几何体,使得它的从正面与上面看到的图形如图所示.他至少需要10个小立方块,最多需要13个小立方块. 如图,⊙O的半径OA=2,弦AD=1,过点D作BD∥OA交⊙O于点B,则BA长为$\sqrt{15}$.
如图,⊙O的半径OA=2,弦AD=1,过点D作BD∥OA交⊙O于点B,则BA长为$\sqrt{15}$. 如图,填空:
如图,填空: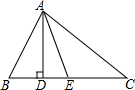 如图在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°,则∠BAE=30°;∠DAE=20°.
如图在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°,则∠BAE=30°;∠DAE=20°.