题目内容
8. 如图,⊙O的半径OA=2,弦AD=1,过点D作BD∥OA交⊙O于点B,则BA长为$\sqrt{15}$.
如图,⊙O的半径OA=2,弦AD=1,过点D作BD∥OA交⊙O于点B,则BA长为$\sqrt{15}$.
分析 延长AO与⊙O交于点C,连结BC,根据BD∥OA,得出BC=AD=1,再根据AC是直径,求出AC,再根据勾股定理即可得出答案.
解答 解:延长AO与⊙O交于点C,连结BC,
∵BD∥OA,
∴BC=AD=1,
∵AC是直径,
∴AC=4,∠ABC=90°,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$
故答案为:$\sqrt{15}$.
点评 此题考查了圆周角定理,用到的知识点是勾股定理和圆周角定理,关键是作出辅助线,构造直角三角形.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
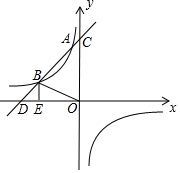 如图,直线y=mx+4交x轴于D,交y轴于C,交双曲线y=$\frac{k}{x}$在第二象限交于点A和点B(-3,n),且S△OBE=$\frac{3}{2}$.
如图,直线y=mx+4交x轴于D,交y轴于C,交双曲线y=$\frac{k}{x}$在第二象限交于点A和点B(-3,n),且S△OBE=$\frac{3}{2}$. 某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元,小王携带现金3000元到这市场购苹果,并以批发价买进,如果购买的苹果为x千克,小王付款后的剩余现金为y元.
某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元,小王携带现金3000元到这市场购苹果,并以批发价买进,如果购买的苹果为x千克,小王付款后的剩余现金为y元. 如图,在△ABC中,∠ABC和∠ACB的外角平分线交于D,∠A=50°,那么∠D=65°.
如图,在△ABC中,∠ABC和∠ACB的外角平分线交于D,∠A=50°,那么∠D=65°.