题目内容
10.甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与x之间的函数图象是( )| A. | 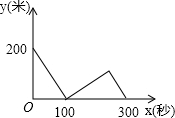 | B. | 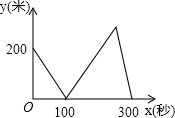 | ||
| C. | 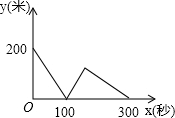 | D. | 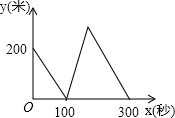 |
分析 先算出甲到达终点的时间,由此算出二者之间的最大距离,再算出乙到达终点的时间,由此找出点的坐标,结合点的坐标利用待定系数法求出函数解析式,根据函数解析式分析四个选项即可得出结论.
解答 解:当甲跑到终点时所用的时间为:2000÷8=250(秒),
此时甲乙间的距离为:2000-200-6×250=300(米),
乙到达终点时所用的时间为:(2000-200)÷6=300(秒),
∴最高点坐标为(250,300).
设y关于x的函数解析式为y=kx+b,
当0≤x≤100时,有$\left\{\begin{array}{l}{b=200}\\{100k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=200}\end{array}\right.$,
此时y=-2x+200;
当100<x≤250时,有$\left\{\begin{array}{l}{100k+b=0}\\{250k+b=300}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=-200}\end{array}\right.$,
此时y=2x-200;
当250<x≤300时,有$\left\{\begin{array}{l}{250k+b=300}\\{300k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-6}\\{b=1800}\end{array}\right.$,
此时y=-6x+1800.
∴y关于x的函数解析式为y=$\left\{\begin{array}{l}{-2x+200(0≤x≤100)}\\{2x-200(100<x≤250)}\\{-6x+1800(250<x≤300)}\end{array}\right.$.
∴整个过程中y与之间的函数图象是B.
故选B.
点评 本题考查了函数的图象,解题的关键是根据点的坐标利用待定系数法求出函数解析式.本题属于基础题,难度不大,解决该题型题目时,找出点的坐标,利用待定系数法求出函数解析式是关键.

| A. | 1-3 | B. | (-1)×3 | C. | 3-1 | D. | (-1)3 |




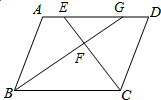 已知:如图,在?ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交CE于点F,交AD于点G.
已知:如图,在?ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交CE于点F,交AD于点G.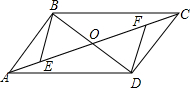 如图,?ABCD的对角线AC、BD相交于点O,OE=OF.
如图,?ABCD的对角线AC、BD相交于点O,OE=OF. 随着生活水平的提高,人们的健康意识、环保意识都在逐步增强,锻炼形式多种多样,跑步、打拳、徒步、广场舞、球类等等,李叔叔每天上班都坚持骑自行车,如图是他从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
随着生活水平的提高,人们的健康意识、环保意识都在逐步增强,锻炼形式多种多样,跑步、打拳、徒步、广场舞、球类等等,李叔叔每天上班都坚持骑自行车,如图是他从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线左侧部分的面积即为t分钟内王叔叔行进的路程s(米).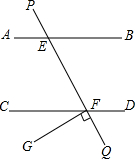 如图,AB∥CD,直线PQ分别交AB、CD于E、F,FG⊥PQ,若∠PEB=130°,求∠CFG的度数.
如图,AB∥CD,直线PQ分别交AB、CD于E、F,FG⊥PQ,若∠PEB=130°,求∠CFG的度数.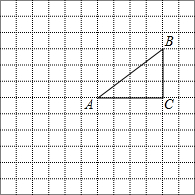 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB′C′.