题目内容
19．
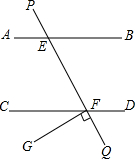如图，AB∥CD，直线PQ分别交AB、CD于E、F，FG⊥PQ，若∠PEB=130°，求∠CFG的度数．
分析 根据对顶角相等得到∠AEF=∠PEB=130°，根据平行线的性质得到∠CFQ=∠AEF=130°，根据垂直的定义得到∠QFG=90°，即可得到结论．
解答 解：∵∠AEF=∠PEB=130°，
∵AB∥CD，
∴∠CFQ=∠AEF=130°，
∵∠FG⊥PQ，
∴∠QFG=90°，
∴∠CFG=∠CFQ-∠GFQ=40°．
点评 本题考查的是平行线的性质，垂直的定义，用到的知识点为：两直线平行，同旁内角互补．
练习册系列答案
相关题目
9．如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题
（1）将下面的表格补充完整：
（2）根据规律，是否存在一个正多边形，其中的∠α=20°？若存在，请求出n的值，若不存在，请说明理由．
（1）将下面的表格补充完整：
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| ∠α的度数 | 60° | 45° | 36° | 30° | … | （$\frac{180}{n}$）° |
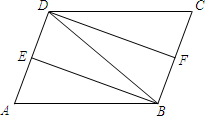如图，在?ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．
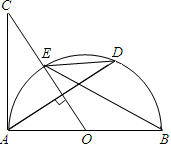如图，AB是⊙O的直径，过圆心O作弦AD的垂线交半⊙O于点E，交AC于点C，使∠BED=∠C．
8．下列图中∠1和∠2是同位角的是（ ）
| A． | ①、②、③ | B． | ②、③、④ | C． | ③、④、⑤ | D． | ①、②、⑤ |
9．
如图，在?ABCD中，AC与BD交于O点，则下列结论中不一定成立的是（ ）
如图，在?ABCD中，AC与BD交于O点，则下列结论中不一定成立的是（ ）| A． | AB=CD | B． | AO=CO | C． | AC=BD | D． | BO=DO |