题目内容
18.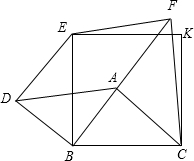 已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.
已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.(1)求证:四边形ADEF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADEF是菱形?请说明理由.
(3)进一步探究:四边形ADEF与四边形EKCB相似的可能性,并求其相似比.
分析 (1)连接EC,如图1,易证△BCA∽△ECF,从而可得EF=$\sqrt{2}$AB=AD,易证△DBE≌△ABC,从而有DE=AC=AF,即可得到四边形ADEF是平行四边形;
(2)当AC=$\sqrt{2}$AB时,可得AD=AC,由AF=AC可得AD=AF,即可得到平行四边形ADEF是菱形;
(3)当AC=$\sqrt{2}$AB且∠BAC=135°时,可证到四边形ADEF是正方形,显然正方形ADEF与正方形EKCB相似.过点B作BN⊥AC,交CA的延长线于点N,如图2,易得∠BAN=45°,AN=BN=$\frac{\sqrt{2}}{2}$AB.设AB=2x,可得AD=2$\sqrt{2}$x,AN=BN=$\sqrt{2}$x,AC=2$\sqrt{2}$x,CN=3$\sqrt{2}$x,BC=2$\sqrt{5}$x,即可求出四边形ADEF与四边形EKCB的相似比.
解答 解:(1)证明:连接EC,如图1.
∵四边形EKCB是正方形,
∴∠EBC=90°,BE=BC,∠BCE=45°,EC=$\sqrt{2}$BC.
∵∠FAC=90°,AC=AF,
∴∠ACF=45°,FC=$\sqrt{2}$AC,
∴∠BCE=∠ACF,$\frac{EC}{FC}$=$\frac{\sqrt{2}BC}{\sqrt{2}AC}$=$\frac{BC}{AC}$,
∴∠BCA=∠ECF,
∴△BCA∽△ECF,
∴$\frac{BA}{EF}$=$\frac{CA}{CF}$=$\frac{1}{\sqrt{2}}$,
∴EF=$\sqrt{2}$AB.
∵∠ABD=90°,AB=DB,
∴AD=$\sqrt{2}$AB,
∴AD=EF.
∵∠ABD=∠EBC=90°,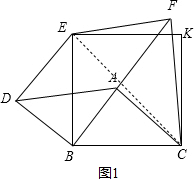
∴∠DBE=∠ABC.
在△DBE和△ABC中,
$\left\{\begin{array}{l}{BD=BA}\\{∠DBE=∠ABC}\\{BE=BC}\end{array}\right.$,
∴△DBE≌△ABC(SAS),
∴DE=AC,
∴DE=AC=AF,
∴四边形ADEF是平行四边形;
(2)当AC=$\sqrt{2}$AB时,四边形ADEF是菱形.
理由:∵AD=$\sqrt{2}$AB,AC=$\sqrt{2}$AB,
∴AD=AC.
∵AF=AC,
∴AD=AF.
∵四边形ADEF是平行四边形,
∴平行四边形ADEF是菱形;
(3)当AC=$\sqrt{2}$AB且∠BAC=135°时,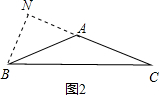
则有四边形ADEF是菱形,且∠DAF=360°-135°-90°-45°=90°,
∴菱形ADEF是正方形,
∴正方形ADEF与正方形EKCB相似.
过点B作BN⊥AC,交CA的延长线于点N,如图2,
则有∠BAN=180°-135°=45°,
∴AN=BN=$\frac{\sqrt{2}}{2}$AB.
设AB=2x,则AD=2$\sqrt{2}$x,AN=BN=$\sqrt{2}$x,AC=2$\sqrt{2}$x,CN=3$\sqrt{2}$x,
∴BC=$\sqrt{B{N}^{2}+C{N}^{2}}$=2$\sqrt{5}$x,
∴正方形ADEF与正方形EKCB的相似比为$\frac{AD}{BC}$=$\frac{2\sqrt{2}x}{2\sqrt{5}x}$=$\frac{\sqrt{10}}{5}$.
点评 本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定、菱形的判定、正方形的判定与性质、勾股定理等知识,综合性比较强,证到△BCA∽△ECF,从而得到EF=$\sqrt{2}$AB=AD是解决第(1)小题的关键.

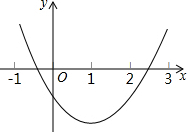 如图是某二次函数的图象,将其向右平移两个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有( )
如图是某二次函数的图象,将其向右平移两个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有( )(1)a>0;(2)c<0;(3)6a+b=0;(4)a+b+c>0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )
已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )| A. | 2sin50° | B. | 2sin40° | C. | 2tan50° | D. | 2tan40° |
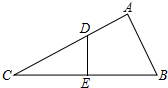 如图所示,在△ABC中,AB=6,AC=8,BC=10,现将它们折叠,使点C与点B重合,DE为折叠,则DE=$\frac{15}{4}$.
如图所示,在△ABC中,AB=6,AC=8,BC=10,现将它们折叠,使点C与点B重合,DE为折叠,则DE=$\frac{15}{4}$.