题目内容
13.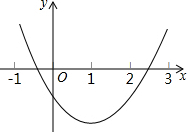 如图是某二次函数的图象,将其向右平移两个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有( )
如图是某二次函数的图象,将其向右平移两个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有( )(1)a>0;(2)c<0;(3)6a+b=0;(4)a+b+c>0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 如图是y=ax2+bx+c的图象,根据开口方向向上知道a>0,又由与y轴的交点为在y轴的正半轴上得到c>0,由对称轴x=-$\frac{b}{2a}$=3,可以得到6a+b=0,又当x=1时,可以判断a+b+c的值.由此可以判定所有结论正确与否.
解答 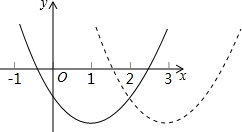 解:(1)∵将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c(a≠0)(如虚线部分),
解:(1)∵将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c(a≠0)(如虚线部分),
∴y=ax2+bx+c的对称轴为:直线x=3;
∵开口方向向上,
∴a>0,故(1)正确;
(2)∵与y轴的交点为在y轴的正半轴上
∴c>0,故(2)错误;
(3)∵对称轴x=-$\frac{b}{2a}$=3,
∴6a+b=0,故(3)正确;
(4)当x=1时,y=a+b+c>0,故(4)正确.
故选C.
点评 本题考查了二次函数y=ax2+bx+c系数符号的确定,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.多项式x2+3x-2中,下列说法错误的是( )
| A. | 这是一个二次三项式 | B. | 二次项系数是1 | ||
| C. | 一次项系数是3 | D. | 常数项是2 |
8.下列实数中属于无理数的是( )
| A. | 3.14 | B. | $\frac{22}{7}$ | C. | π | D. | $\sqrt{9}$ |
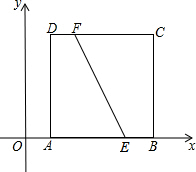 如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).
如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).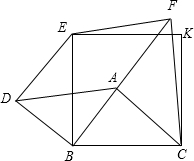 已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.
已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.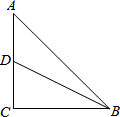 在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则:
在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则: