题目内容
8.先化简,再求值:(a-b)(a+2b)+(6ab3-2a2b2)÷2ab,其中a=2,b=-1.分析 先算乘法和除法,再合并同类项,最后代入求出即可.
解答 解:(a-b)(a+2b)+(6ab3-2a2b2)÷2ab
=a2+2ab-ab-2b2+3b2-ab
=a2+b2,
当a=2,b=-1时,原式=22+(-1)2=5.
点评 本题考查了整式的混合运算和求值的应用,能正确运用整式的法则进行化简是解此题的关键,难度适中.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
19.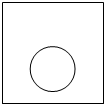 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )| A. | πr2 | B. | a2-πr2 | C. | 4r2-πr2 | D. | $\frac{a^2}{4}$ |
16.已知方程$\frac{x}{2}-\frac{y}{3}=5$,用含x的代数式表示y,下列给出的结论中正确的是( )
| A. | $x=\frac{2y}{3}+10$ | B. | $y=\frac{3x}{2}-15$ | C. | $y=\frac{3x-15}{2}$ | D. | $y=-\frac{3x}{2}+15$ |
17.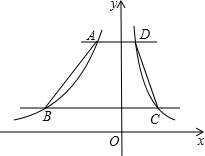 如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
 如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )| A. | 点A的横坐标是-$\frac{3}{5}$,点B的横坐标是-3 | |
| B. | 点A的横坐标是-$\frac{3}{5}$,点B的纵坐标是$\frac{4}{3}$ | |
| C. | 点A的纵坐标是$\frac{16}{3}$,点B的横坐标是-3 | |
| D. | 点A的纵坐标是$\frac{16}{3}$,点B的纵坐标是$\frac{4}{3}$ |
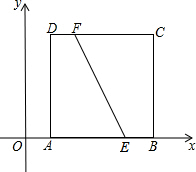 如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).
如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0). 如图,将一副三角板的直角顶点重合,可得∠COA=∠DOB,理由是同角的余角相等;若∠AOD=50°,则∠COB=130°.
如图,将一副三角板的直角顶点重合,可得∠COA=∠DOB,理由是同角的余角相等;若∠AOD=50°,则∠COB=130°.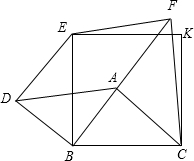 已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.
已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.