题目内容
10.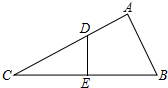 如图所示,在△ABC中,AB=6,AC=8,BC=10,现将它们折叠,使点C与点B重合,DE为折叠,则DE=$\frac{15}{4}$.
如图所示,在△ABC中,AB=6,AC=8,BC=10,现将它们折叠,使点C与点B重合,DE为折叠,则DE=$\frac{15}{4}$.
分析 如图,首先证明CD=BD(设为λ),则AD=8-λ;其次证明∠A=90°;在△ABD中,运用勾股定理列出关于λ的方程,求出λ;再次运用勾股定理求出DE的长,即可解决问题.
解答 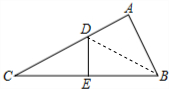 解:如图,连接BD;由题意得:
解:如图,连接BD;由题意得:
CD=BD(设为λ),则AD=8-λ;
CE=BE=5;在△ABC中,
∵62+82=102,
∴∠A=90°;由勾股定理得:
λ2=(8-λ)2+62,
解得:λ=$\frac{25}{4}$;由勾股定理得:
DE2=BD2-BE2,
解得:DE=$\frac{15}{4}$.
故答案为$\frac{15}{4}$.
点评 该题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的方法是准确找出图形中隐含的等量关系;解题的关键是灵活运用翻折变换的性质等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
1.多项式x2+3x-2中,下列说法错误的是( )
| A. | 这是一个二次三项式 | B. | 二次项系数是1 | ||
| C. | 一次项系数是3 | D. | 常数项是2 |
 如图,将一副三角板的直角顶点重合,可得∠COA=∠DOB,理由是同角的余角相等;若∠AOD=50°,则∠COB=130°.
如图,将一副三角板的直角顶点重合,可得∠COA=∠DOB,理由是同角的余角相等;若∠AOD=50°,则∠COB=130°.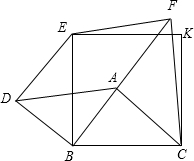 已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.
已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.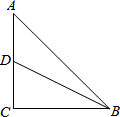 在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则:
在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则: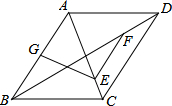 如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.
如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.