题目内容
(1)如图,在等腰梯形ABCD中,AB∥CD,点M是AB的中点.求证:△ADM≌△BCM.
(2)如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,
(1)若以点B为平面直角坐标系为原点,以BC所在的直线为x轴建立平面直角坐标系,则点C的坐标为 ,点A的坐标为 ;
(2)将△ABC绕点B顺时针旋转90°到△A′B′C′的位置,在图中画出旋转后得到的△A′B′C′;
(3)在(2)中求线段AB扫过的图形面积是多少平方单位(结果保留π).
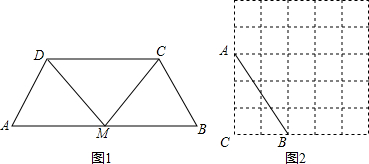
(2)如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,
(1)若以点B为平面直角坐标系为原点,以BC所在的直线为x轴建立平面直角坐标系,则点C的坐标为
(2)将△ABC绕点B顺时针旋转90°到△A′B′C′的位置,在图中画出旋转后得到的△A′B′C′;
(3)在(2)中求线段AB扫过的图形面积是多少平方单位(结果保留π).
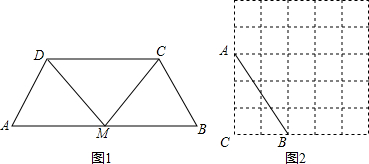
考点:作图-旋转变换,全等三角形的判定,等腰梯形的性质
专题:
分析:(1)先根据等腰三角形的性质得出AD=BC,∠A=∠B,再由点M是AB的中点得出MA=MB,故可得出△ADM≌△BCM;
(2)①以点B为原点,以BC所在的直线为x轴建立坐标系,根据AC两点在坐标系中的位置写出两点坐标即可;
②根据图形旋转的性质画出旋转后的△A′B′C′即可;
③根据扇形的面积公式即可得出结论.
(2)①以点B为原点,以BC所在的直线为x轴建立坐标系,根据AC两点在坐标系中的位置写出两点坐标即可;
②根据图形旋转的性质画出旋转后的△A′B′C′即可;
③根据扇形的面积公式即可得出结论.
解答: (1)证明:在等腰梯形ABCD中,AB∥CD
(1)证明:在等腰梯形ABCD中,AB∥CD
∴AD=BC,∠A=∠B
∵点M是AB的中点
∴MA=MB
在△ADM与△BCM中,
,
∴△ADM≌△BCM(SAS);
(2)①由图可知,C(-2,0),A(-2,3).
故答案为:(-2,0),(-2,3);
②如图所示:
③∵AB=
=
,
∴S扇形BAA′=
=
π.
 (1)证明:在等腰梯形ABCD中,AB∥CD
(1)证明:在等腰梯形ABCD中,AB∥CD∴AD=BC,∠A=∠B
∵点M是AB的中点
∴MA=MB
在△ADM与△BCM中,
|
∴△ADM≌△BCM(SAS);
(2)①由图可知,C(-2,0),A(-2,3).
故答案为:(-2,0),(-2,3);
②如图所示:
③∵AB=
| 22+32 |
| 13 |
∴S扇形BAA′=
90π(
| ||
| 360 |
| 13 |
| 4 |
点评:本题考查的是作图-旋转变换,熟知图形旋转的性质是解答此题的关键.

练习册系列答案
相关题目
若⊙O的面积为25π,在同一平面内有一个点P,且点P到圆心O的距离为4.9,则点P与⊙O的位置关系为( )
| A、点P在⊙O外 |
| B、点P在⊙O上 |
| C、点P在⊙O内 |
| D、无法确定 |
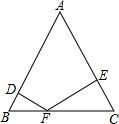 如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.
如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.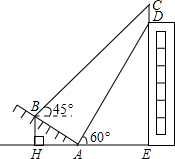 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
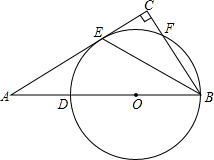 如图,Rt△ABC中,∠C=90°,D在AB上,BE平分∠ABC交AC于点E,以BD为直径的圆经过点E,交BC于点F.
如图,Rt△ABC中,∠C=90°,D在AB上,BE平分∠ABC交AC于点E,以BD为直径的圆经过点E,交BC于点F.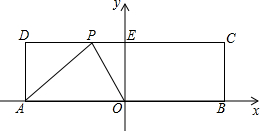 如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.
如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标. 如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.
如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.