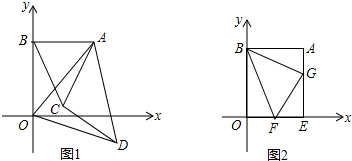题目内容
 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:| 3 |
考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:过B作DE的垂线,设垂足为G.分别在Rt△ABH中,通过解直角三角形求出BH、AH,在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长,然后根据CD=CG+GE-DE即可求出宣传牌的高度.
解答:解:过B作BG⊥DE于G,
Rt△ABH中,i=tan∠BAH=
=
,
∴∠BAH=30°,
∴BH=
AB=5;
∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵BH=5,AH=5
,
∴BG=AH+AE=5
+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5
+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=
AE=15
.
∴CD=CG+GE-DE=5
+15+5-15
=20-10
≈2.7(m).
答:宣传牌CD高约2.7米.

Rt△ABH中,i=tan∠BAH=
| 1 | ||
|
| ||
| 3 |
∴∠BAH=30°,
∴BH=
| 1 |
| 2 |
∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵BH=5,AH=5
| 3 |
∴BG=AH+AE=5
| 3 |
Rt△BGC中,∠CBG=45°,
∴CG=BG=5
| 3 |
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=
| 3 |
| 3 |
∴CD=CG+GE-DE=5
| 3 |
| 3 |
| 3 |
答:宣传牌CD高约2.7米.
点评:此题综合考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若双曲线y=
与直线y=2x+1的一个交点的横坐标为-1,则k的值为( )
| k |
| x |
| A、-1 | B、1 | C、-2 | D、2 |
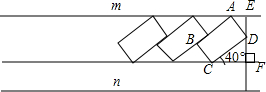 某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.
某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.| A、8.6 | B、5.2 |
| C、4.8 | D、5.6 |
 如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )
如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )| A、1:2 | B、2:3 |
| C、1:4 | D、2:5 |
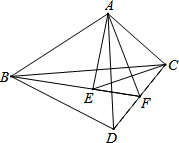 如图,△ABC,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①BE=CD;②FA平分∠EFC;③FE=FD;④FE+FC=FA;其中一定正确的结论有( )个.
如图,△ABC,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①BE=CD;②FA平分∠EFC;③FE=FD;④FE+FC=FA;其中一定正确的结论有( )个.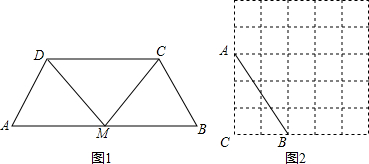
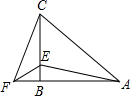 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.