题目内容
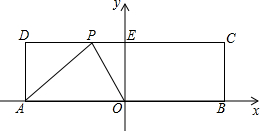 如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.
如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.考点:等腰三角形的判定,坐标与图形性质,勾股定理
专题:
分析:根据点A、B、C的坐标求出OA、BC、CE,再分①点A的顶角顶点,利用勾股定理列式求出DP,再求出EP,然后写出点P的坐标;②点O是顶角顶点,利用勾股定理列式求出EP,再分点P在第一象限和第二象限两种情况写出点P的坐标.
解答:解:∵A(-5,0),B(5,0),C(5,3),
∴OA=OB=5,BC=3,CE=5,
①若点A的顶角顶点,由勾股定理得,DP=
=4,
所以,PE=5-4=1,
所以,点P的坐标为(-1,3),
②若点O是顶角顶点,由勾股定理得,EP=
=4,
所以,点P的坐标为(-4,3)或(4,3),
综上所述,点P的坐标为(-1,3)或(-4,3)或(4,3).
∴OA=OB=5,BC=3,CE=5,
①若点A的顶角顶点,由勾股定理得,DP=
| 52-32 |
所以,PE=5-4=1,
所以,点P的坐标为(-1,3),
②若点O是顶角顶点,由勾股定理得,EP=
| 52-32 |
所以,点P的坐标为(-4,3)或(4,3),
综上所述,点P的坐标为(-1,3)或(-4,3)或(4,3).
点评:本题考查了等腰三角形的判定,坐标与图形性质,勾股定理,难点在于根据等腰三角形的顶点分情况讨论.

练习册系列答案
相关题目
 如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )
如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )| A、1:2 | B、2:3 |
| C、1:4 | D、2:5 |
 如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=
如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=| 2 |
A、2
| ||
B、2
| ||
C、3
| ||
D、4
|
对于抛物线y=-(x-1)2+2,下列说法中错误的是( )
| A、对称轴是直线x=1 |
| B、顶点坐标是(1,2) |
| C、当x>1时,y随x的增大而减小 |
| D、当x=1时,函数y的最小值为2 |
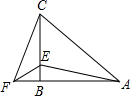 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.