题目内容
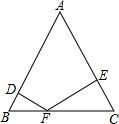 如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.
如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.(1)求证:△BDF∽△CEF;
(2)设BF=m,四边形ADEF面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值.
考点:相似三角形的判定与性质,二次函数的最值,等边三角形的性质
专题:
分析:(1)只需找到两组对应角相等即可.
(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,借助三角函数用m表示出AD、DF、AE、EF的长,进而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题.
(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,借助三角函数用m表示出AD、DF、AE、EF的长,进而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题.
解答:(1)求证:∵DF⊥AB,EF⊥AC,
∴∠BDF=∠CEF=90°.
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,
∴△BDF∽△CEF.
(2)解:∵∠BDF=90°,∠B=60°,
∴sin60°=
=
,cos60°=
=
.
∵BF=m,
∴DF=
m,BD=
m.
∵AB=4,
∴AD=4-
m.
∴S△ADF=
AD•DF
=
×(4-
m)×
m
=-
m2+
m.
同理:S△AEF=AE•EF=-
m2+2
.
∴S=S△ADF+S△AEF
=-
m2+
m+2
=-
(m2-4m-8)
=-
(m-2)2+3
∴当m=2时,S取最大值,最大值为3
.
∴∠BDF=∠CEF=90°.
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,

∴△BDF∽△CEF.
(2)解:∵∠BDF=90°,∠B=60°,
∴sin60°=
| DF |
| BF |
| ||
| 2 |
| BD |
| BF |
| 1 |
| 2 |
∵BF=m,
∴DF=
| ||
| 2 |
| 1 |
| 2 |
∵AB=4,
∴AD=4-
| 1 |
| 2 |
∴S△ADF=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=-
| ||
| 8 |
| 3 |
同理:S△AEF=AE•EF=-
| ||
| 8 |
| 3 |
∴S=S△ADF+S△AEF
=-
| ||
| 4 |
| 3 |
| 3 |
=-
| ||
| 4 |
=-
| ||
| 4 |
| 3 |
∴当m=2时,S取最大值,最大值为3
| 3 |
点评:本题考查了相似三角形的判定、二次函数的最值、三角函数、解直角三角形、等边三角形的性质等知识,综合性强,灵活掌握并运用基础知识解决问题.

练习册系列答案
相关题目
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 0025米,把0.000 0025用科学记数法表示为( )
| A、2.5×106 |
| B、0.25×10-5 |
| C、25×10-7 |
| D、2.5×10-6 |
若双曲线y=
与直线y=2x+1的一个交点的横坐标为-1,则k的值为( )
| k |
| x |
| A、-1 | B、1 | C、-2 | D、2 |
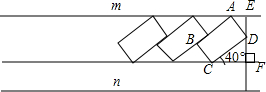 某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.
某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.| A、8.6 | B、5.2 |
| C、4.8 | D、5.6 |
 如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )
如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )| A、1:2 | B、2:3 |
| C、1:4 | D、2:5 |
 如图,在平面直角坐标系xOy中,边长为
如图,在平面直角坐标系xOy中,边长为