题目内容
 如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.
如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.考点:全等三角形的判定与性质
专题:证明题
分析:根据垂直的定义得到∠ABC=∠EDC=90°,则可根据”SAS“判定△ABC≌△CDE,根据三角形全等的性质得∠A=∠DCE,利用∠ACB+∠A=90°可得∠ACB+∠DCE=90°,再利用平角的定义计算出∠ACE=90°,
然后根据垂直的定义即可得到结论.
然后根据垂直的定义即可得到结论.
解答:证明:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠EDC=90°,
在△ABC和△CDE中,
,
∴△ABC≌△CDE,
∴∠A=∠DCE,
∵∠ACB+∠A=90°,
∴∠ACB+∠DCE=90°,
∴∠ACE=90°,
∴AC⊥CE.
∴∠ABC=∠EDC=90°,
在△ABC和△CDE中,
|
∴△ABC≌△CDE,
∴∠A=∠DCE,
∵∠ACB+∠A=90°,
∴∠ACB+∠DCE=90°,
∴∠ACE=90°,
∴AC⊥CE.
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
若双曲线y=
与直线y=2x+1的一个交点的横坐标为-1,则k的值为( )
| k |
| x |
| A、-1 | B、1 | C、-2 | D、2 |
对于抛物线y=-(x-1)2+2,下列说法中错误的是( )
| A、对称轴是直线x=1 |
| B、顶点坐标是(1,2) |
| C、当x>1时,y随x的增大而减小 |
| D、当x=1时,函数y的最小值为2 |
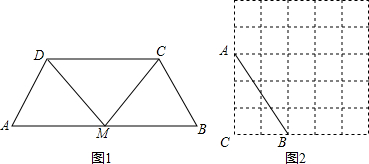
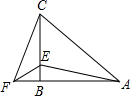 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.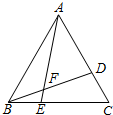 已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=
已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=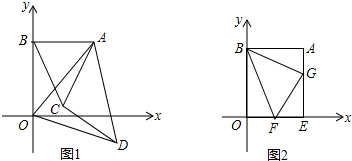
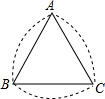 如图所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作
如图所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作